|
By Kardi Teknomo, PhD.
< Previous | Index | Next >
Several interesting concepts we presented in our paper are as follow:
-
Generalized Origin-Destination (OD) matrix is the superset of
traditional Origin-Destination matrix in which every node in the network is
considered as either source or sink. Generalized OD can be obtained and updated
from tracking devices installed in probe vehicles such as public utilities
vehicles, taxis and commercial vehicles as well as private cars.
- Given trajectories on the physical network from any tracking
devices such as GPS, mobile phone, RFID, blue tooth, video camera and soon, it
is possible to obtain the flow matrix and generalized origin destination matrix
directly from these trajectories. We presented two algorithms to obtain the
flow matrix and generalized origin destination matrix from trajectories.
- Transportation network can be categorized into two parts: the
network structure (such as physical road network or pedestrian network) and the
network utilization (how the network is utilized by agents such as cars or
pedestrians).
- The network structure is represented by adjacency matrix
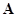 , path
matrix , path
matrix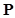 , external matrix , external matrix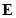
- The network utilization is represented by generalized origin-destination
matrix
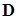 , flow matrix , flow matrix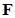 , alternative route matrix , alternative route matrix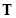 and substitute
route flow matrix and substitute
route flow matrix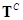 and desire lines or indirect flow matrix and desire lines or indirect flow matrix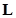 . .
- Adjacency matrix is a subset of path matrix and therefore
adjacency matrix is always less than or equal to path matrix
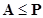 . .
- Therefore, we can get the difference between adjacency matrix and
path matrix, to what I called as External Matrix
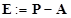 . .
- Flow-set matrix is a subset of the corresponding
Generalized Origin-Destination-set matrix and therefore Flow matrix is
less than or equal to generalized origin destination matrix
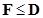
- Desire line in transportation network can be drawn based on indirect flow matrix
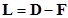 . .
- When there is no alternative route flow, we can find the
relationship between network structure and network utilization as simple as
element wise product of the matrices
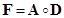 . .
- When there is alternative route flow, we can find the
relationship between network structure and network utilization as simple as
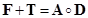 . .
- Alternative route flow matrix
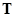 counts the number of
agents that pass through other routes other than the corresponding direct link. counts the number of
agents that pass through other routes other than the corresponding direct link.
- More comprehensive relationship between network structure and
network utilization are given by the following formulas which proofs can be
found in the paper.
< Previous | Index | Next >
These tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi. (2013) Relationship between Generalized Origin Destination and Flow Matrix – A Tutorial
http://people.revoledu.com/kardi/research/trajectory/od/ |