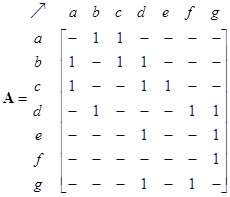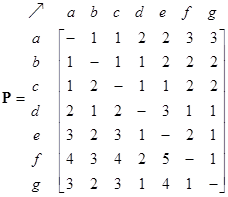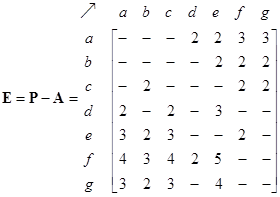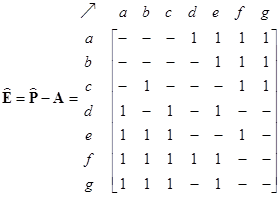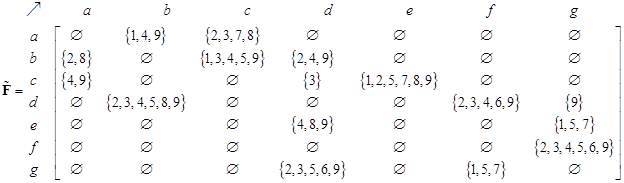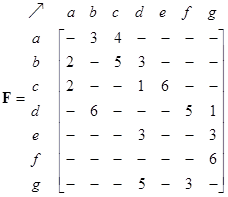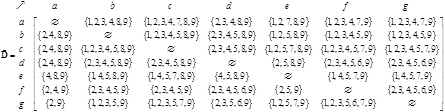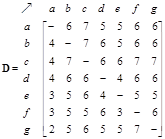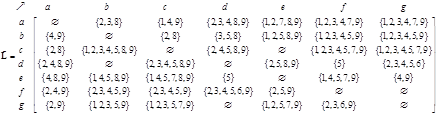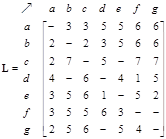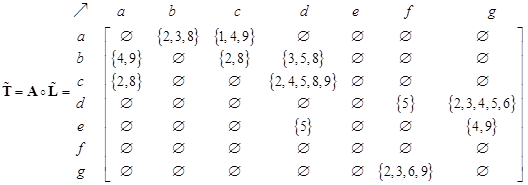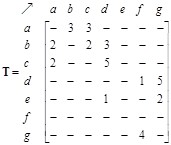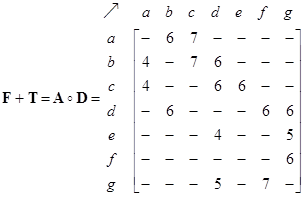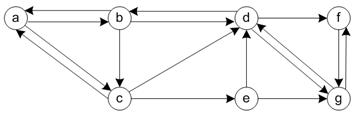
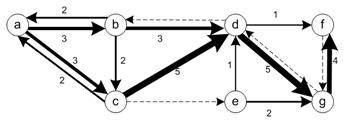
General Network Graph Numerical Example

By Kardi Teknomo, PhD.

< Previous | Index | Next >

The second numerical illustration involves a simple but general network with 7 nodes and 16 directed links. We also generate 9 arbitrary ordinal graph simple trajectories (without loop) to be placed in the network. Every link on the network is passed by at least one trajectory.

The network structure can be represented by 3 types of matrices: adjacency matrix, path matrix and external matrix. The adjacency matrix of the network is shown below together with its path matrix. Zeros in the matrices are deleted so that the reader can see the pattern of the matrix structure better. Notice that the non-zero and non-infinity entries are located on non-diagonal positions of the path matrix to indicate that there is path from any node to any other nodes in the network. The diagonals are zero because we do not have internal self-loop structure.

The external matrix is obtained from the path matrix by removing the direct links structure (i.e. adjacency matrix).  In this case, we eliminate all one entries from the path matrix. The matrix-structure can be enhanced by binarizing the matrix.

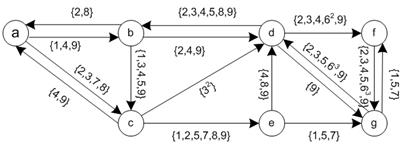
In utilizing the network, we now put the nine trajectories of our example into the network.Note that the 3 loops in trajectory #6. In the sketch the trajectory number is drawn as an exponent to show the number of loops to the readers. In the matrix set of trajectories and the computation, however, the loop on trajectory is simply represented as single loop in the set because members of a set are unique. This representation makes sense because our ordinal graph trajectory actually comes from dynamic trajectory. The agent will not be present more than once in a given link at a given time. Therefore, a unique representation of each trajectory is necessary.

Flow set matrix indicates the trajectory ids that pass through direct links in the network. Empty set elements occur when there is no direct link.

Counting the number of elements in each set of the flow set matrix produces flow matrix that can be visualized using a flow pattern.

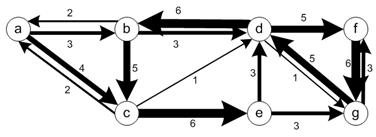
Intersecting the trajectory sets that go out of a node and trajectories that go in to a node produces OD- set matrix. For instance, trajectory #1 of a->b->c->e->g->f will produce origin destination pair nodes of {a->b, a->c, a->e, a->g, a->f, b->c,b->e, b->g,b->f, c->e, c->g, c->f, e->g, e->f, g-f}. Putting the trajectory id into the OD pair nodes produces origin-destination-set matrix. OD matrix simply counts the number of elements of the OD set matrix.

Desire-line set matrix is obtained from the set difference between OD-set matrix and flow-set matrix. For instance, trajectory ids {1,2,3,4,8,9} are passing node a to node b, however, only trajectory ids {1, 4,9} are passing direct link . The remaining trajectories {2,3, 8} are using other alternative route to go from node a to node b.

Taking only parts of direct links from the desire-line-set matrix, we obtain alternative route flow set matrix. Notice that not all direct links have alternative route flow. For instance, links,,and  have only direct link flows without alternative route flows (because no trajectory is passing through those OD pairs using alternative route).

The alternative route flow matrix is simply the count of the members of set. The visualization of alternative flow matrix is also shown.

In this numerical example, it is clear that the relationship of following equation holds because

< Previous | Index | Next >

Share and save this tutorial

 

These tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. (2013) Relationship between Generalized Origin Destination and Flow Matrix – A Tutorial
http://people.revoledu.com/kardi/research/trajectory/od/