<
Previous
|
Next
|
Contents
>
What is Mean or Average?
Phillips
(2000) defined the mean of two real positive numbers,
![]() and
and
![]() as a mapping or function of the two numbers into a real positive number
as a mapping or function of the two numbers into a real positive number
![]() . The mapping must satisfy three properties:
. The mapping must satisfy three properties:
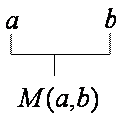
-
If
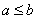 then
then
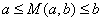 . The mean value always lies between the two numbers.
. The mean value always lies between the two numbers.
-
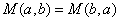 . Mean is symmetric in
. Mean is symmetric in
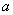 and
and
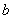
-
If
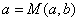 then
then
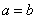
Other properties of Mean:
4.
Homogeneous mean
will satisfy one additional property
![]() . Examples of homogeneous mean are arithmetic mean, geometric mean and harmonic mean.
. Examples of homogeneous mean are arithmetic mean, geometric mean and harmonic mean.
5. If
![]() , then
, then
![]() . This property happens because of the first property. Note that the property number 3 is the exact contrary of this property number 5.
. This property happens because of the first property. Note that the property number 3 is the exact contrary of this property number 5.
Expanding for more than two numbers, I may generalize the three properties of mean and the definition of mean. Mean is defined as a mapping or function of the real positive numbers into a real positive number that satisfy property that the mean value always lies between the input numbers .
Three Properties that defined Mean:
-
If we have numbers
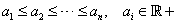 , then
, then
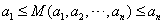
-
The order of input numbers is not important. Mean is symmetric in
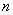 dimension. Example:
dimension. Example:
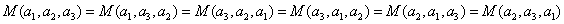
-
If all inputs are equal, then the mean value is equal to any one of its input. From property number 1 we can deduce that if
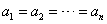 then
then
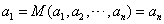
Note:
- Mean is defined only for real positive number input. No negative numbers is allowed as input
-
The number of input is finite up to
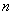 (not infinite)
(not infinite)
- The mean value is somewhere in between the lowest and the highest input numbers. The mean value will not go outside this range of input.
- Actually, the symmetric property of mean is not a necessary condition. Others may define unsymmetrical mean.
<
Previous
|
Next
|
Contents
>
Rate this tutorial or give your comments about this tutorial
See also:
Kolmogorov's Generalized Mean
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Mean and Average. https:\\people.revoledu.com\kardi\tutorial\BasicMath\Average\
