Linear Transformation of a Complex Number
Suppose we have a set of complex points
and we have two complex numbers
and
then we can obtain another set of complex points
using linear transformation
This complex linear transformation is rigid body transformation which contains a rotation about the origin and a scaling and a translation.
Properties of Complex Linear Transformation
-
Complex number
controls the scaling by scale of
and the rotation through angle
. For positive rotation angle we have
,
-
Complex number
translate the results of multiplication of
into
.
Example:
Suppose we have these set of complex points that produce a shape.
The plot of Real and Imaginary of the complex points is shown below as a complex plane.
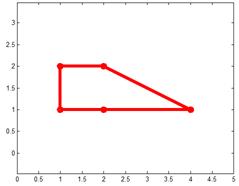
We want to design a complex linear transformation that will rotate
counterclockwise and scale it at 0.5 and translate it (0.5, 1)
Answer
We want to find the value of
such that
and
. For the translation, we simply use
.
We know that
and
.
Thus, we have
and
. However, the range of function tan in computer is usually from -pi to +pi, thus, we need to adjust by shifting pi/2 to get the correct result.
From trigonometry, we know that
. Thus, we have
and
We input the second equation to the first equation to give
-->
-->
Thus,
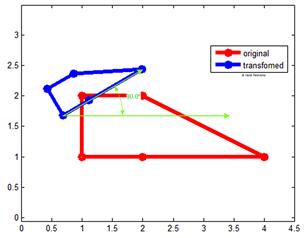
See Also : Fractal Geometry , Application of Complex Number
Rate this tutorial or give your comments about this tutorial