Other name: Cyclic continued fraction; recurring chain fraction
Periodic continued fraction is defined as a infinite continued fraction where
for some fixed integer
and
for all
. We put bar notation to represent the part of the sequence that repeated infinitely.
Notation
is the periodic part that repeated infinitely, thus
The cyclic continued fraction is proven convergence (see
Phillips, 2000
)
Step by step to compute the convergence limit of periodic continued fraction analytically is as follow
1. Identify the periodic terms and set it as
2. Compute the periodic term as continued fraction using difference equation
,
and get the ratio of the last two convergent
and
3. Solve quadratic equation
and select positive
4. Compute continued fraction
using difference equation above.
Example
Calculate cyclic continued fraction
!
The periodic terms are
. To compute the convergence of this periodic term we set
,
,
,
. Then we set quadratic equation
, or
, or
. Factoring the quadratic equation, we have positive
. Then we compute continued fraction
=
. Using the same difference equation again we have
,
,
,
. Thus, the convergence limit of the continued fraction
is
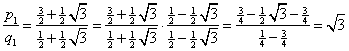
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Continued Fraction. http://people.revoledu.com/kardi/tutorial/ContinuedFraction/index.html