Digital root of prime numbers

By Kardi Teknomo, PhD.

< Previous | Next | Contents >

Pattern of Digital Root of Prime Number

In this section, I describe my exploration on the pattern of digital root of prime number.

Prime numbers are integers that have only factors: 1 and the number itself. The list of the first few primes : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, ...

All primes are odd numbers except 2. Number 2 is the only even prime.

How about digital root of primes? Can we find a pattern from the digital root of primes?The list of the first few primes with its digital root:

Then the pattern of the first 15 primes is 235724815241572

The list of the first 664,579 primes number (that is primes below 10 million) with its digital root and additive persistence can be downloaded as a text file here (Warning: file size 32.3 MB).

Based on that limited number of primes and its digital root, I would say that the digital root of prime numbers does not form any cyclical or repeated pattern. You can download the pattern of digital root of the first 664,579 primes here (1.3 MB).

Here are my conjectures regarding digital root of prime numbers:

1. The pattern of digital root of prime number is chaotic (I am not sure how to prove this?)
2. Number 3 (which of course the digital root is also 3) is the only prime that has digital root 3 (surprise!)
3. There no prime has digital root of 6 and 9.
4. Digital root of prime numbers are almost equally distributed among (1, 2, 4, 5, 7, 8), about 1/6 (limiting behavior in the long run)

Of course, my conjectures above are based only on a few primes (only 664,579 primes) and there is no guarantee that conjectures above are true for a very large prime.

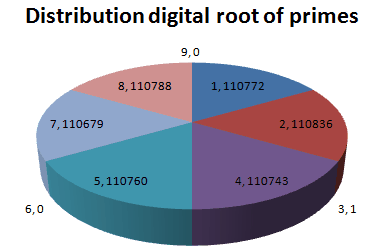
Here is the distribution of the digital root of prime number

After analyzing the pattern of digital root of prime number, I have more questions than answers. Some of the few crucial questions would be:

• Is there any way to find cyclical pattern of a large number?
• Since prime number seems to be infinite, how to proof that my conjectures above are correct or false?
• Is there a cleverer way to find digital root of very large prime number?
• Why there is only one prime has digital root of 3
• Why there is no prime has digital root of 6 and 9?

Note from Karan Chandigarh, India (August 18, 2014):

First of all you have to understand the divisibility of any number by '3'. There is a very interesting pattern of number 3 and digital root. If you want to check the divisibility of a number then there is a short cut for it. You have to just take the digital root of a number then we have to check whether that number is divisible by '3' or not. If the digital root of that number is divisible by '3' then original number is also divisible by '3' if not then that is not a multiple of '3'.

For example:-

a) 15 = Digital root of 15 is 6 (1+5) and 6 is divisible by '3' so the original number is also divisible by '3' i.e 15/3 =5

b) 7569 = Digital root of 7569 is 9 (7+5+6+9) and 9 is divisible by '3' so the original number is also divisible by '3' i.e. 7569/3 =2523

c) 991114 = Digital root of 991114 is 7 and 7 is NOT divisible by '3' so the original number is also not divisible by '3' i.e 991114/3= 330371.33

Above divisibility rule of '3' is universal which could be apply to any number starting from 1 to infinity. You have to understand the above explaination before moving to the below answers.

Now,

One of your questions is :- Why there is only one prime number has digital root of '3' ?

Answer : If a prime number other than '3' has a digital root '3' then that is divisible of '3' SO there is no such prime number exist! That is why in our number line only '3' is the only prime number whose digital root is '3'! Like 2 is the only prime even number.

Your other question is :- Why there is no prime number whose digital root of '6' and '9' ?

Answer : If a number whose digital root is divisible by '3' then that is always divisible by '3' so a number whose digital root is '6' and '9' then it must be divisible by 1,3 and the number itself ,so, it cannot be a prime number.

< Previous | Next | Contents >

These tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2005). Digital Root. https:\\people.revoledu.com\kardi\tutorial\DigitSum\