Share this: Google+
Solving Inequality using Excel
In this tutorial, we will use MS Excel Goal Seek to solve the inequality of the following equation
In other word, we want to find
that satisfy above in inequality equation above.
Download the spreadsheet example here
.
To solve this inequality equation, first use left hand side of the equation as function
and then graph this function. The graph is shown in the figure below. At x = 0, the function is infinity.
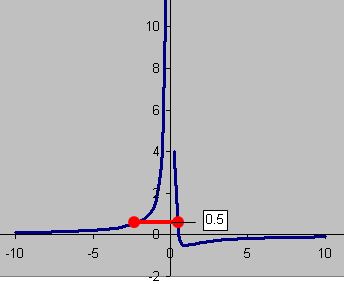
Clearly, from the graph the value of the function is
for an interval x around -3 to +0.5. Our problem is to find this boundary. Using MS Excel Goal Seek, we can solve this problem easily. If you need the
spreadsheet example, you can download for free here.
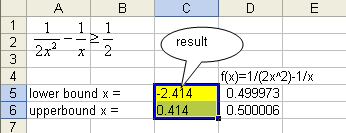
- Suppose the initial guess of the lower bound is inputted in cell C5 and the initial guess of upper boundary is in cell C6. Let the initial guess of lower boundary is -5 and the initial guess for upper boundary of x is 0.5.
-
Type the equation of
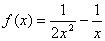for both boundaries in D5 and D6 respectively. D5 = 1/(2*C5^2)-1/C5, D6 = 1/(2*C6^2)-1/C6
3. We solve the two boundaries one at a time. From the menu of MS Excel, click Tools-Goal Seek and Goal Seek dialog show up.
4. Set cell D5 ( the function equation ) to value 0.5 ( target value of inequality ) by changing cell $C$5 ( initial guess of lower boundary ) and click OK button
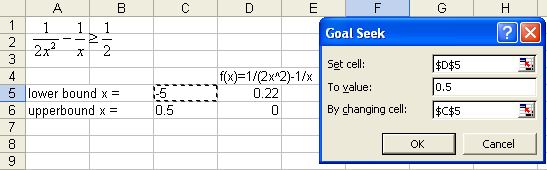
5. Repeat the procedure for upper boundary. Set cell D6 ( the function equation ) to value 0.5 ( target value of inequality ) by changing cell $C$6 ( initial guess of upper boundary ) and click OK button
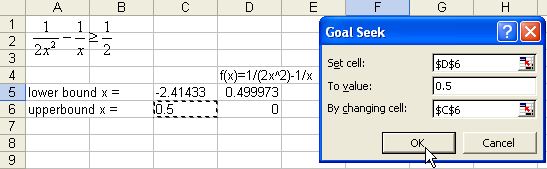
6. The results are shown in the figure below. The inequality equation
is satisfied by this interval
See also:
Goal Seek Tutorial
,
MS Excel Tutorial index
,
Kardi Teknomo's Tutorial
Send your comments, questions and
suggestions
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Solving inequality using Microsoft Excel Goal Seek. https:\\people.revoledu.com\kardi\ tutorial\Excel\SolvingInequalityGoalSeek.html