Comparison Numerical Solution of ODE

< Previous | Next | Contents >

Comparison of Runge Kutta Methods

The exact general solution of the example 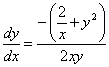is . Inputting the initial value gives and the particular solution is . From initial value, this solution only exist in the range up to about because beyond that the right hand side is negative and square root of negative number give complex number.

Plot of all the four Runge-Kutta method and the exact solution is given below

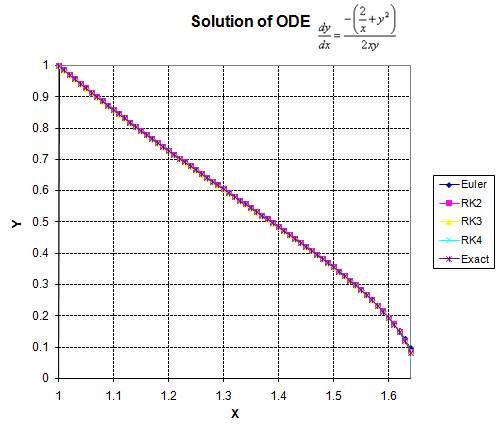
Note that the numerical solutions of the four methods as well as the exact solution produce almost the same results. When there is a gap between the numerical solution and the exact solution, this gap usually can be narrowed by setting smaller value of .

Though the exact solution does not exist after , the numerical solutions still produce some results but the four methods produce different results. Care must be taken to ensure that you use the domain that produces solution.

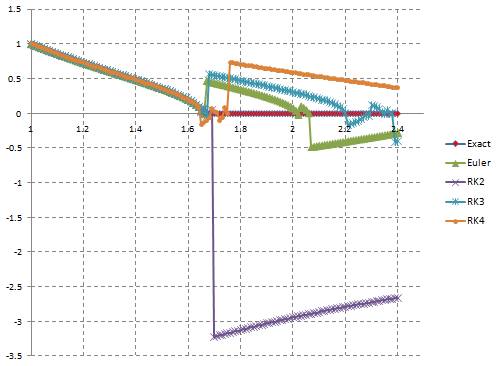
< Previous | Next | Contents >

See also: Numerical Excel tutorial , Dynamical System tutorial , Kardi Teknomo's Tutorial

Rate this tutorial

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Solving Ordinary Differential Equation (ODE). https:\\people.revoledu.com\kardi\tutorial\ODE\