Second Order Runge-Kutta Method (RK2) to Solve ODE

By Kardi Teknomo, PhD .

< Previous | Next | Contents >

Runge Kutta-2

Suppose we have ODE then

Formula :

Where

and

Other variation name : Improve Euler method, Heun's method, Midpoint method

Error term : , correct up to the second order term in Taylor series expansion.

The Taylor series expansion is

The computation is using spreadsheet that can be downloaded here

Example:

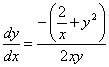, set , with initial condition . The few first results and the graph of solution are given below.

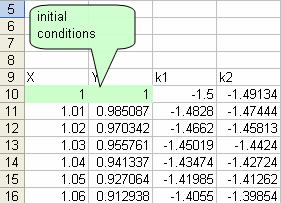
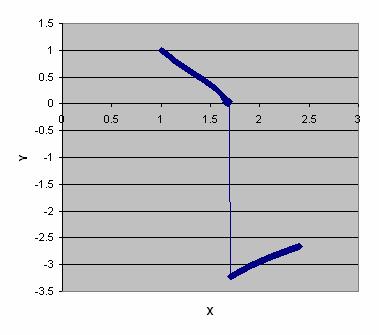
Note that after , the solution is not correct. See Comparison.

Expanding the order Runge-Kutta formula, we have

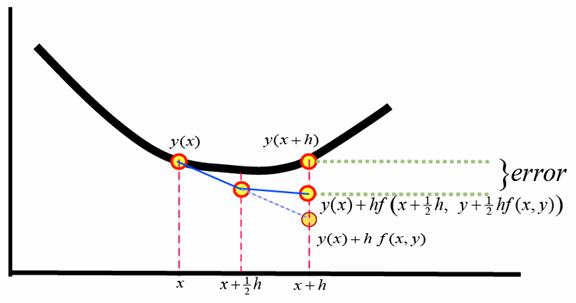
Second term of the right hand side [ ] is the estimated range difference. The estimated range difference is computed based on a half of the slope at the beginning of the interval and the slope in the middle of the interval , as illustrated in the figure below

Rate this tutorial

< Previous | Next | Contents >

See also: Numerical Excel tutorial , Dynamical System tutorial , Kardi Teknomo's Tutorial

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Solving Ordinary Differential Equation (ODE). https:\\people.revoledu.com\kardi\ tutorial\ODE\