<
Previous
|
Next
|
Contents
>
Whatis ODE?
Ordinary differential equation (ODE) is an equation that involves a rate of change of a dependent variable with respect to
one
independent variable. The rate of change is denoted by one of these equal notations
. Suppose we have a function
, then variable
is called
domain
or
independent
variable and variable
is called
range
or
dependent
variable.
Because the rate change is involved only one variable, we call it ordinary derivative. This is in contrast to partial derivatives that involves rate of change of several variables. That is why we have ordinary differential equation (ODE) in contrast to partial differential equation (PDE).
Example:
is an ordinary differential equation with respect to one variable
. The ODE is said to have 3-rd order because the highest order of the rate is 3. It is a first degree ODE because the power of the highest order is 1.
The following example illustrates the meaning of solution to differential equation.
Example:
Suppose we have a function
. Differentiate this equation gives an ODE
. Thus the
general solution
of ODE
is
. When we know the value of
, we say that the
particular solution
of the ODE is
. Notice that we reverse the strategy from solution to equation.
The general equation of the first order Ordinary Differential Equation (ODE) is given as
The right hand side is a function
, which usually may involve the independent variable
, the dependent variable
and constants. Sometimes, either variable
or
are constant and it may simplify the case. In case the dependent variable
is not presence, the right hand side becomes function
and the solution of differential equation can be solved immediately by integration.
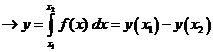
Example below illustrates a case when both variable
or
are constants such that
.
Example:
Suppose we found that population of our region has a constant rate of growth. If we put notation
for the number of population in the region at time
(measured in year), we can equate a constant growth rate with equation
. Suppose we know that the growth rate is
and this year population is 1200 people. What is the number of population 10 years from now? To answer that question we need to solve the ODE
, which will give answer
, inputting
gives answer
When the dependent variable
in the right hand side of general ODE equation
is not a constant, the integration is not straightforward as above example. It needs differential algebraic equation as shown in the example below.
Example:
Solve
for
with initial value
As you may have learn in Calculus, we can write the equation as
. We can separate
and
such that
. Integrate both side of the equation
we get
or
, or
. We can input initial condition
into
we get
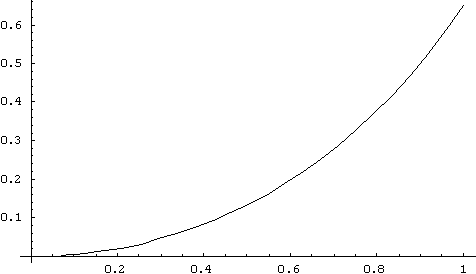
. Thus, the solution is
. We plot for the range of x between 0 and 1
<
Previous
|
Next
|
Contents
>
See also: Numerical Excel tutorial , Dynamical System tutorial , Kardi Teknomo's Tutorial
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Solving Ordinary Differential Equation (ODE). https:\\people.revoledu.com\kardi\tutorial\ODE\