<
Previous
|
Next
|
Contents
>
Quadratic Function
First, let us distinguish several similar terms. What is the different between quadratic function from quadratic equation and quadratic formula?
Function
is called
quadratic function
when the three parameters
,
and
are real numbers. Quadratic function is more general function than a
linear function
because when the value of parameter
, then the quadratic function degenerate becomes a linear function
(linear means straight line geometrically). When the function value is set to be equal to zero (i.e.
), the quadratic function is called
quadratic equation
.
The formula to find the roots of quadratic equation is called quadratic formula
or often called ABC formula because it involves three parameters
,
and
.
We will explore more the three quadratic terms above. First, we discuss about the characteristics of quadratic function.
Geometrically, quadratic function
produces a parabola curve when we plot in
plane. The shape and characteristics of the quadratic function is closely related to the parabola and depends on the value of the parameters.
|
|
|
|
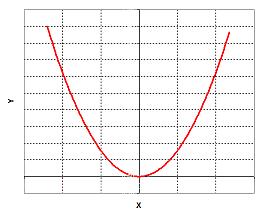
Smiling parabola when
|
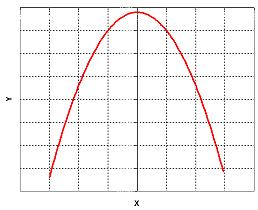
Sad parabola when
|
-
The parameter attached to the quadratic term (
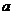) is called
quadratic parameter or shape parameter
because it influences the shape of the parabola. When the quadratic parameter is positive (
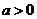), the parabola is opened upward, look like a smile (it is sometimes called
concave up
). The lowest or highest point on the parabola is called
extreme point
. For a smiling parabola, the extreme point is at minimum.
-
When the quadratic parameter is negative (
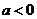), the parabola is opened downward, look like a sad mouth (it is sometimes called
concave down
). The extreme point of sad parabola is at maximum.
-
Of course, if the quadratic parameter is zero (
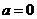), the quadratic function becomes linear function and has no extreme point.
-
The second parameter (
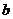) is the
gradient
of linear function degenerated from quadratic function.
-
If we input
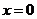to quadratic function
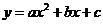, we get an
intercept
or a crossing point (at
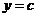) between parabola curve and vertical axis. Thus, the third parameter (
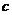) determine the intercept point. If
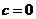then the parabola will pass the origin
.
-
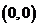The extreme point is at coordinate
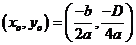where
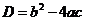is called
discriminant
of quadratic equation. We will discuss more about discriminant in the
next section
. The vertical line passing the extreme point
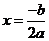divides the parabola symmetrically into two parts. Therefore, this vertical line is called
axis of symmetry
.
Quadratic function may appear in several forms. Below are the forms that are typically found in many applications.
-
Polynomial form
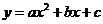. This is the general form that we are using throughout the tutorial
-
Standard form
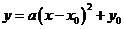where
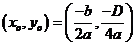is the extreme point (maximum or minimum point) where
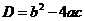. We will discuss the application example of extreme point in
later section
. Inputting the coordinate of extreme point to the standard form yield general polynomial form
3. Factored form
where
and
are the roots of the quadratic equation where
and
. Inputting the roots into the factored form produces general polynomial form.
In the next section, you will learn about quadratic equation.
<
Previous
|
Next
|
Contents
>
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2019) Quadratic Function Tutorial .
http://people.revoledu.com/kardi/tutorial/quadratic/