Divisibility
Division is an interesting arithmetic operation. Given positive integers, not all number can be divided by the other number. Division by zero is undefined. Some real number such as square root of 3 cannot be obtained by dividing one integer into another.
An integer number M is called divisor of N if there is no remainder when N is divided by M.
For example:
- The divisors of 32 are 1, 2, 4, 8, 16, and 32.
- The divisors of 12 are 1, 2, 3, 4, 6 and 12.
- The divisors of 11 are 1 and 11.
Now, how can you find the list of divisors of say 12345? You probably need a computer to compute that. The algorithm below will help you to find out that the divisors of 12345 are 1, 3, 5 15, 823, 2469, 4115, and 12345. Here is a challenge for you: how many divisors do 12345677890 have? Can you list them all?
Before we discuss about the algorithm to find divisors, you need to learn several arithmetic operations that closely related to division.
When a number 25 is divided by 7 it produces quotient 3 and leaves a remainder 4. The 25 is called dividend and 7 is called divisor.
Division operation
say that
a
is divided by
m
produces quotient
q
and a remainder
r
.
Operator
div
(is called integer division) produce quotient:
For example:
The computation of integer division in computer (if the programming language does not provide) is using floor function after division
In code:
function IntDiv(nominator, denominator)
{
return Math.floor(nominator/denominator);
}
Another operator, called Modulus or Mod in short, gives the remainder of division:
For example: 25 mod 7 = 4
The computation of modulus operator in computer is usually provided in the programming language. In case your programming language does not provide this operator, mod operation computes the remainder as
In code:
function Remainder(nominator, denominator)
{
return nominator-denominator*IntDiv(nominator, denominator);
}
An integer number N is divisible by an integer number M if the remainder of division is zero (no remainder).
Example:
- 9 is divisible by 3, thus we can say that 9 mod 3 = 0
- 9 is not divisible by 2 because 9 mod 2 = 1, that is 9/2 = 4 with remainder 1
- 32 is divisible by 8. 32 mod 8 is 0
The following online program will determines the quotient and remainder of division
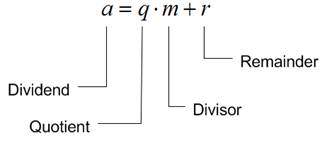
in the form of
a = q.m+r
By now we are ready to make the code to list all divisors of an integer. We can use Mod operation to find all divisors of a positive integer. The pseudo code below will list all the divisors of a number N in an array
Having the code to find the divisors of an integer, now you dare to try to list all divisors of quite a big number. For example if you run the code above for N = 1234567 we will obtain the divisors of 1234567 are 1, 127, 9721 and 1234567.
You can challenge yourself to find out what is the list of divisors of 123456789?
Using code above, which is not efficient code, it may need several second to compute (and freeze your computer for a while). More efficient code will test only integer between 1 and square root of N (do it yourself for your exercise using that clue).
The answer is 1, 3, 9, 3607, 3803, 10821, 11409, 32463, 34227, 13717421, 41152263, 123456789. Next, you may try 12345677890.
Play around with the following online program of divisor. This program will count the number of divisors and list all the divisors of a positive integer number.
In the next section, you will learn about prime number which has been interest of many great mathematicians for more than 2000 years!