Hierarchical Clustering Tutorial: Cophenetic Coefficient

Cophenetic Coefficient

How good is the clustering that we just performed? There is an index called Cross Correlation Coefficient or Cophenetic Correlation Coefficient (CP) that shows the goodness of fit of our clustering similar to the Correlation Coefficient of regression.

To compute the Cophenetic Correlation Coefficient of hierarchical clustering, we need two informations:

Distance matrix
Cophenetic Matrix

We have distance as the input for Hierarchical clustering computation. Because distance matrix is symmetric, for our purpose, we need only the lower triangular values

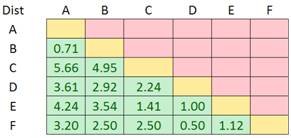
distance matrix

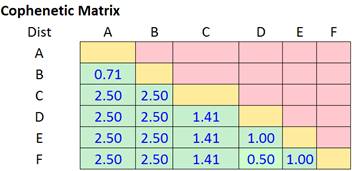
To obtain Cophenetic matrix, we need to fill the lower triangular distance matrix with the minimum merging distance that we obtain in the previous section. Remember in our summary of last section,

We merge cluster D and F into cluster (D, F) at distance 0.50
We merge cluster A and cluster B into (A, B) at distance 0.71
We merge cluster E and (D, F) into ((D, F), E) at distance 1.00
We merge cluster ((D, F), E) and C into (((D, F), E), C) at distance 1.41
We merge cluster (((D, F), E), C) and (A, B) into ((((D, F), E), C), (A, B)) at distance 2.50

Using this information, we can fill the Cophenetic Matrix into

cophenetic matrix

Now we got the two required information and we can put them together into a single matrix.

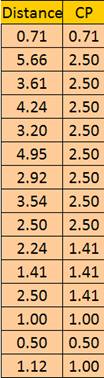
correlation

Cophenetic Correlation Coefficient is simply correlation coefficient between distance matrix and Cophenetic matrix =Correl (Dist, CP) = 86.399%. As the value of the Cophenetic Correlation Coefficient is quite close to 100%, we can say that the clustering is quite fit.