Multiplication of Two Complex Numbers
If we have two complex numbers
and
then we can multiply them together
and
then we can multiply them together
then we can multiply them together
Example
and
and
It is simpler to represent complex multiplication in polar form. If
and
then
and
then
then
-
The magnitude is
. Multiplication of two complex number produces magnitude of the product length of the two factors.
. Multiplication of two complex number produces magnitude of the product length of the two factors.
-
The direction is
. Multiplication of two complex number produces sum of angles of the two factors.
. Multiplication of two complex number produces sum of angles of the two factors.
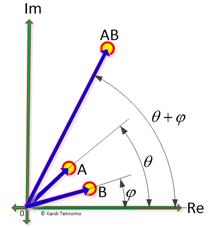
Graphically, complex multiplication is represented by polar form representation illustrated below. Geometrically multiplying a complex number
with a complex number
will
scale
the length of
by the amount of
and then
rotate
it with amount of
about the origin counterclockwise.
with a complex number
will
scale
the length of
by the amount of
and then
rotate
it with amount of
about the origin counterclockwise.
will
scale
the length of
by the amount of
and then
rotate
it with amount of
about the origin counterclockwise.
by the amount of
and then
rotate
it with amount of
about the origin counterclockwise.
and then
rotate
it with amount of
about the origin counterclockwise.
about the origin counterclockwise.
Complex Number Calculator
Properties of Complex Multiplication
-
Commutative
-
Associative
-
Distributive
-
Complex number
is the identity element of complex multiplication because
.
is the identity element of complex multiplication because
.
.
-
Factor theorem: the product of two complex number cannot be zero unless at least one of the two is itself a zero. If
is zero complex number, then
implies either
or
, or both.
is zero complex number, then
implies either
or
, or both.
implies either
or
, or both.
or
, or both.
, or both.
-
Multiplication of a real number with a complex number will affect both real and imaginary part. Let
be a real number and
is a complex number. Then,
be a real number and
is a complex number. Then,
is a complex number. Then,
-
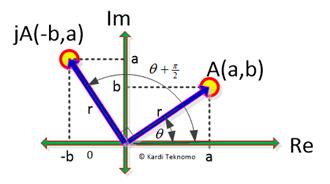
Multiplication of imaginary number
with a complex number
produces
which geometrically means a counterclockwise rotation by a right angle.
with a complex number
produces
which geometrically means a counterclockwise rotation by a right angle.
produces
which geometrically means a counterclockwise rotation by a right angle.
which geometrically means a counterclockwise rotation by a right angle.
See Also : Complex Division , Complex Addition , Complex Subtraction
Rate this tutorial or give your comments about this tutorial