Magnitude nd Direction of a Complex Number
There are two ways to represent a point in a plane. One way is using Cartesian coordinate and the other way is using polar coordinate. Using Cartesian coordinate, a complex number is represented as a single point in the complex plane,
. Using Polar coordinate, a complex number is represented as a vector with magnitude and direction.
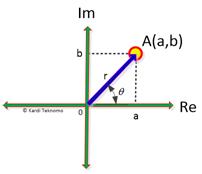
The direction is measured as an angle in radians. Positive angle is measured counterclockwise from the positive real axis. The directed angle is called argument of the complex number.
The magnitude of a complex number is the length of vector
. The magnitude is sometimes called
amplitude
,
modulus
or
absolute value
of complex number
.
The direction of vector
is given by
We can also write for the angle itself as argument of the complex number
Note that you must care about the quadrant in which the complex number lies by computing the correct signed value of the angle.
Complex Number Calculator
Properties
-
Real part inequalities
. It will become equal when the imaginary parts is zero.
-
Imaginary part inequality
. It will become equal when the real parts is zero.
See Also : Complex Conjugate , Arithmetic of Complex Number
Rate this tutorial or give your comments about this tutorial