Decimal to Fraction Conversion

By Kardi Teknomo, PhD .

< Previous | Next | Content >

How do we obtain approximation ratio of a real number? Suppose you have a number with several decimal digits like this: 2.14567, what is the best rational approximation of this number? What is the error of this approximation? Try the Decimal to Rational number calculator below.

Of course, we can always say that 2.14567 = 214567/100000 without any approximation. However, some number like may not have the exact decimal number and we can use approximation of continued fraction using this simple algorithm:

Algorithm:

Suppose we have a decimal number

At the beginning, we compute term, error and reciprocal of remainder respectively as

, ,

Then continued the iteration with iteration formula

, , , for to

Once we get the term of continued fraction, we can use the difference equation , to get the ratio

The iteration is stop when the absolute error is very small

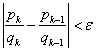, and we report the result of one iteration before.

Example (hand calculation):

, and we set accuracy we want to get the fraction approximation.

We start with making a continued fraction. We use difference equation with initial condition , , ,

,

,

, (by definition), then with absolute error 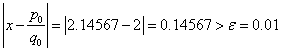, thus we continue the iteration

The first iteration we have

, ,

, , then with absolute error 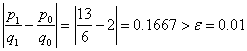, thus we continue the iteration

The second iteration we have

, ,

, , then with absolute error 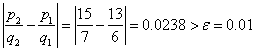, thus we continue the iteration

The third iteration we have

, ,

, , then with absolute error 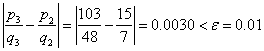, thus we stop the iteration and report the conversion of decimal with remainder

Implementation Code

Visual Basic code for this conversion is given below

Function Decimal2Fraction(ByVal decNum As Double, ByVal accuracy As Double, _ 

ByRef nominator, ByRef denominator, ByRef remainder) 

' Input decNum always between zero to 1 

' copyright (c) Kardi Teknomo 2006-2023

' http://people.revoledu.com/kardi

Dim a(25) ' I assume the accuracy is lower than 25 digit decimals 

Dim y(25), r(25) 

Dim p(25), q(25) 

Dim error 

Dim i As Integer, k As Integer 

Dim ratio As Double, prevRatio As Double 

For k = 0 To 24 

If k = 0 Then 

a(0) = Int(decNum) ' function Int in VB is equivalent to Floor 

r(0) = decNum - a(0) 

If r(0) <> 0 Then y(0) = 1 / r(0) 

p(0) = a(0) 

q(0) = 1 

ratio = p(0) / q(0) 

error = Abs(decNum - ratio) 

Else 

a(k) = Int(y(k - 1)) ' function Int in VB is equivalent to Floor 

r(k) = y(k - 1) - a(k) 

y(k) = 1 / r(k) 

If k = 1 Then 

p(1) = a(1) * p(0) + 1 

q(1) = a(1) * q(0) 

Else 

p(k) = a(k) * p(k - 1) + p(k - 2) 

q(k) = a(k) * q(k - 1) + q(k - 2) 

End If 

ratio = p(k) / q(k) 

error = Abs(ratio - prevRatio) 

End If 

If error < accuracy Then 

Exit For 

Else 

prevRatio = ratio 

End If 

Next k 

' report the results 

nominator = p(k - 1) 

denominator = q(k - 1) 

remainder = r(k - 1) 

Decimal2Fraction = nominator / denominator 

End Function 

Try the online interactive program that use the above Decimal to Fraction code so that you can see the code in action.

Alternatively, you may use the program or spreadsheet companion of this tutorial to get conversion of any decimal numbers. For example, try interesting number such as and try different accuracy

< Previous | Next | Content >

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Continued Fraction. http://people.revoledu.com/kardi/tutorial/ContinuedFraction/index.html