Newton Raphson Using Microsoft Excel

by Kardi Teknomo

Newton Raphson method is one of the most famous numerical methods to find root of equation . The algorithm is iterative using difference equation

You need to find initial value near to the solution.

To demonstrate the method, we will use MS Excel in two ways to do the iteration. The first way is using spreadsheet and the second way is using MS Excel iteration.

Download the spreadsheet example of this tutorial here.

Example, we want to find the square root of a number, say . Let us name this number as . Let be the square root we are looking for, then or equivalent to . The first derivative is . To solve this using spreadsheet table, we make a table as shown in the figure below

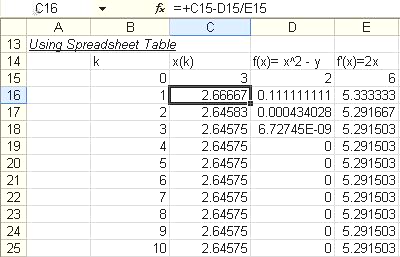
We set any initial value say and compute the and . Then, we use Equation 1 to calculate . Copy and paste these formulas to many rows below, then you get the result because is tend to be convergence to a number of 2.6457.

To use MS Excel iteration, first, use Tools-Options: Calculation Tab, check Iteration check box

1. Type the formulas of 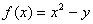, 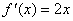and input x(k) = x(0) as the initial value. The result is shown in the figure below

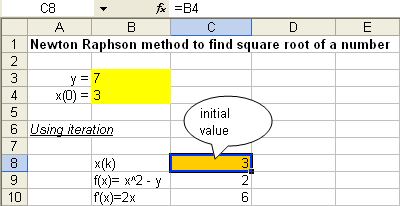
2. After that, type the formula of Newton Raphson in C8 = C8-C9/C10

3. Press F9 to recalculate. You get the result as shown in the figure below

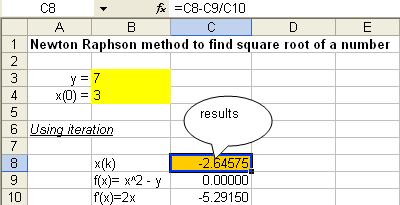
Note that most of iteration procedures are sensitive to initial condition. For example, if you input the initial condition of -5, you may get negative result as the square root which is incorrect.

Unlike spreadsheet way, the iteration procedure is only work for one time usage only. Next time you want to recalculate, you need to do all the steps above again.

See also:
Goal Seek Tutorial, MS Excel Tutorial index, Kardi Teknomo's Tutorial

Send your comments, questions and suggestions

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. Newton Raphson Using Microsoft Excel. http:\\people.revoledu.com\kardi\ tutorial\Excel\NewtonRaphson.html