Linear Discriminant Analysis (LDA) Formula
If there are
groups, the Bayes' rule is minimize the total error of classification by assigning the object to group
which has the highest conditional probability where
. Since we cannot get
(i.e. given the measurement, what is the probability of the class) directly from the measurement and we can obtain
(i.e. given the class, we get the measurement and compute the probability for each class), then we use Bayes Theorem:
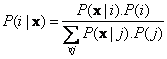
Thus, the Bayes' Rule becomes:
Assign the object to group
if
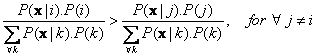
The denominators for both sides of inequality are positive and the same, therefore we can cancel them out to become
Assign the object to group
if
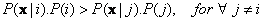
If we have many classes and many dimension of measurement which each dimension will have many values, the computation of conditional probability
requires a lot of data. It is more practical to assume that the data come from some theoretical distribution. The most widely used assumption is that our data come from Multivariate Normal distribution which formula is given as
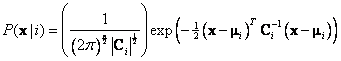
Where,
is vector mean and
is covariance matrix of group i. Inputting the distribution formula into Bayes rule we have:
Assign object with measurement
to group
if
Since factor of
are equal for both sides, we can cancel out
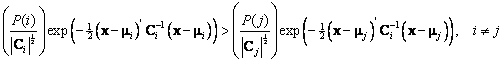
Take logarithmic of both sides
Multiply both sides with -2, we need to change the sign of inequality
Let
we have
Assign object with measurement
to group
if
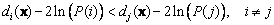
That is Quadratic Discriminant function
If all covariance matrices are equal
, then we can simplify further into
We can write
into
. Thus, the inequality becomes
We can cancel out the first and third terms (i.e.
and
) of both sides because they do not affect the grouping decision. Thus, we have
We multiply both sides of inequality with
(the sign of inequality reverse because we multiply with negative value), we have
Let
, we have
Assign object with measurement
to group
if
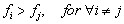
That is Linear Discriminant function
Thus, Linear Discriminant Analysis has assumption of Multivariate Normal distribution and all groups have the same covariance matrix.
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Discriminant Analysis Tutorial. http://people.revoledu.com/kardi/ tutorial/LDA/