Elementary Row Operations
In linear algebra, there are 3 elementary row operations. The same operations can also be used for column (simply by changing the word “row” into “column”). The elementary row operations can be applied to a rectangular matrix size m by n.
- Interchanging two rows of the matrix. Notation
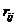means to interchange row 
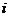and row
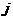. - Multiplying a row of the matrix by a scalar. Notation
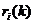means to multiply row 
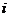by
, 
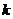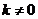. - Add a scalar multiple of a row to another row. Notation
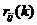means to add 
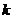times the row
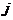to row
,
.
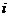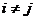Applying the three elementary row operations to a matrix will produce row equivalent matrix. When we view a matrix as augmented matrix of a linear system, the three elementary row operations are equivalent to interchanging two equations, multiplying an equation by a non-zero constant and adding a scalar multiple of one equation to another equation. Two linear systems are equivalent if they produce the same set of solutions. Since a matrix can be seen as a linear system, applying the 3 elementary row operations does not change the solutions of that matrix.
The 3 elementary row operations can be put into 3 elementary matrices. Elementary matrix is a matrix formed by performing a single elementary row operation on an identity matrix. Multiplying the elementary matrix to a matrix will produce the row equivalent matrix based on the corresponding elementary row operation.
Elementary Matrix Type 1: Interchanging two rows of the matrix
,
,
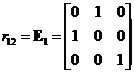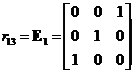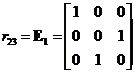
Elementary Matrix Type 2: Multiplying a row of the matrix by a scalar
,
, 
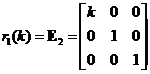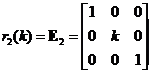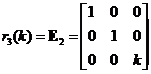
Elementary Matrix Type 3: Add a scalar multiple of a row to another row
,
, 
,
,
, 
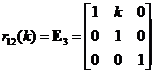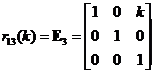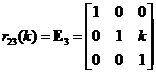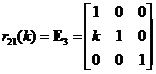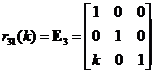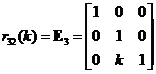
Example:
Suppose we have matrix
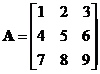
Applying elementary matrix type 3 of 
produces row equivalent matrix
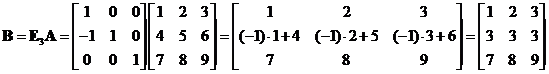
Applying elementary matrix type 2 of 
to the last result produces row equivalent matrix
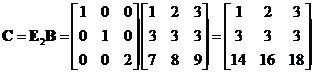
Applying elementary matrix type 1 of 
to the last result produces row equivalent matrix
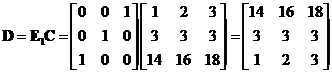
See also: Matrix RREF, Matrix Inverse using Gauss Jordan, matrix rank
Rate this tutorial or give your comments about this tutorial
Preferable reference for this tutorial is
Teknomo, Kardi (2011) Linear Algebra tutorial. https:\\people.revoledu.com\kardi\tutorial\LinearAlgebra\