Cross Product

By Kardi Teknomo, PhD .
LinearAlgebra

< Next | Previous | Index >

Vector Cross Product

Vector cross product is also called vector product because the result of the vector multiplication is a vector. It can only be performed for two vectors of the same size.

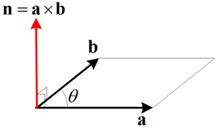
Geometrically, when you have two vectors on a plane, the cross product will produce another vector perpendicular to the plane span by the two input vectors.

The direction of the cross product vector is following the direction of the thumb finger in your right hand when the four other fingers indicate the angle from the first vector to the second vector, as shown in the following figures.


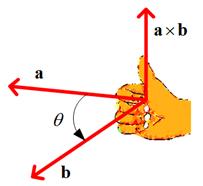
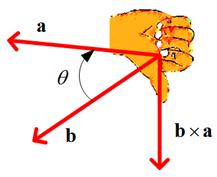
Cross Product Cross Product

Computation of cross product

For 1 or two dimensional vector, the cross product produces zero vectors because they do not make a plane yet. Starting from 3 dimensions, the cross product can be computed algebraically using simple arrangement and a simple rule below

The arrangement to compute vector cross product
1. Arrange the vector as row vector with the first input vector in second position and the second input vector in the third position
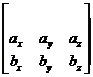
Cross Product
2. Put notation of vector element in the first position
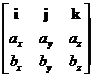
Cross Product
3. Repeat the arrangement on the right
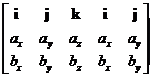
Cross Product

Simple rule to compute cross product

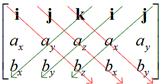
After the arrangement above, multiply the elements of the vectors in diagonal direction and then minus with the product of elements in counter diagonal direction

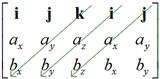
Cross Product Cross Product
Cross Product Cross Product
Now we put them together
Cross Product Cross Product

Unit vector Cross Product represent the first, second and third position of vector elements. Thus, here is the final result
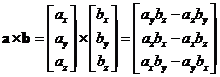
Cross Product

Example
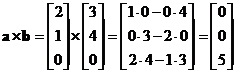
Cross Product

The interactive program of cross product below shows the cross product of two vectors of the same dimension. The program will also show you the internal computation so that you can check your own manual computation. If you click "Random Example" button, the program will generate random input vectors in the right format.

vector a vector b

In the applications, cross product is useful for constructing coordinate system in 3-dimensional space.

Properties

Some important properties of vector cross product are

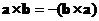
  • Vector cross product is a not commutative operation. If you reverse the order you will get the same magnitude but opposite direction Cross Product
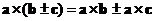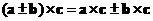
  • Vector cross product is a distributive operation. You can distribute (and group) the vectors with respect to addition or subtraction such that Cross Product and Cross Product
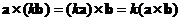  • Vector cross product is an associative operation with respect to scalar multiple of vector. You can exchange the order of computation (operation inside parentheses are to be computed first) does not change the result Cross Product .
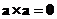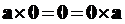  • Vector cross product to itself always produces zero vector Cross Product . Cross product with a zero vector also produces zero vector Cross Product .
  • The magnitude of vector cross product is equal to the product of their norms and sine angle between the two vectors, 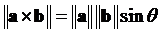Cross Product . This magnitude is equal to the area of parallelogram bounded by the input vectors.
    Cross Product
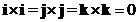
  • Cross product of the same standard unit vector is zero Cross Product
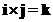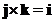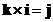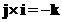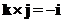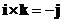  • Cross product of the perpendicular standard unit vector form a cycle Cross Product ; Cross Product ; Cross Product ; Cross Product ; Cross Product ; Cross Product ;
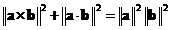  • Relationship of norm of cross product and dot product is Cross Product .

See also : triple dot product , triple cross product , scalar triple product , inner product

< Next | Previous | Index >

Rate this tutorial or give your comments about this tutorial

This tutorial is copyrighted .