Vector Subtraction
Two vectors of the same dimension (i.e. the same number of elements) can be subtracted from one another to produce a resultant vector that is also at the same dimension as the input vectors. Negative vector is a vector with the same magnitude as the input vector but with the opposite direction. Thus vector subtraction is equal to addition of the first vector to the negative of the second vector.
Algebraically, vector subtraction is done by subtracting the corresponding element of the vectors
.
Example
,
,
Geometrically, a line segment bounded by two points
and
is equal to vector subtraction of the two points.
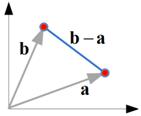
Subtraction of two vectors is equal to
addition
of the first vector to the negative of the second vector. Since a vector can be displaced to a parallel line to the line of application (i.e. a line containing the vector), we can reverse the direction of the second vector and displace it to a parallel line such that we can join the final point of the first vector to the initial point of the second vector as shown in the figure below.
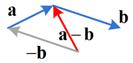
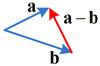
The interactive program below show you the algebraic part of the vector subtraction. Your input must be two vectors of the same dimension (one vector for each text box) and the program will produce the result of vector subtraction.
Properties
Some important properties of vector subtraction are
-
Vector subtraction is a non-commutative operation. If you can reverse the order you will not get the same result
-
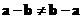
The only vector equal to its own negative is the zero vector and the sum of a vector with its negative is the zero vector,
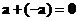
See also
:
vector addition
<
Next
|
Previous
|
Index
>
Rate this tutorial or give your comments about this tutorial