By Kardi Teknomo, Ph.D.

This tutorial introduce you with efficient methods to compute simple statistics such as time average and time variance of any measurement data. Other useful method to revive back your original data from the statistics is also explained.

Preferable reference for this tutorial is

Teknomo, Kardi. Recursive Simple Statistics Tutorial. https:\\people.revoledu.com\kardi\ tutorial\RecursiveStatistic\

Topics

Usual Computation of� Average and Variance
Problems with the usual computational method
Recursive Time-Average
Characteristics of Time Average
Recursive Time-Variance
Data Revival from the Statistics

Usual Computation of� Average and Variance

Suppose you have the following data: 4, 6, 12, 9 and you want to calculate the simple statistics of average (arithmetic mean) and variance, how do you calculate that?

Average =

Variance =

Our focus in particular tutorial is for the time average and time variance of the measurement data. Let us use symbols to ease the algebraic manipulation. Symbol denotes the data number -th. The subscript represent the order of the data when it comes out. In our example above, , , and . Notation represents the average while represents variance of the -th data. In symbolic notation, we say that the usual way to compute the time average is

(1)

While the time variance is

(2)

Now let us consider a case when you have a device to measure something, say number of pedestrians passing through a gate of a subway stations. Every measurement time, for example, every minutes, you get the total number of people who pass through that gate. At each time (i.e. every minutes), you get an additional data and you need to calculate those simple statistics of average and variance of the measurement. How do you calculate them?

Let us use the same data as above for our example. The first measurement, give 4 person passed through the gate. The average is the same as the measurement and there is no variance because we have only single data. The second, third and fourth measurement, give 6, 12 and 9 pedestrians respectively who passed through the gate. The average and variance calculation is shown in the table below.

So far there is nothing interesting to be discussed about unless if we got so much measurement data. All of sudden, the computation of simple statistics of time average and time-variance become problems.

Problems with the usual computational method

Did you see the problem in the usual computation above? Suppose the device above will measure for 24 hours for a week, then you will get 7 times 24 times 60 minutes = 10,080 measurements. If the device is used to measure number of pedestrians for years, then we have so much data. As the number of data is increasing, the number of computation of the simple statistics become very large. If you have number of data, for every measurement , you need to sum all of the data to get the average and then you need to subtract each data from the average and square them, and sum all of those square to get the variance.

Not only the number of computation become large, the memory to store all of those data also become very large. If you only need the statistics, and not the real measurement data, you still need to store all of above measurement data to compute the statistics. Is there a better way than above computation?

The answer is yes. Using recursive time average and time variance you can perform the computation much more efficient without storing all the data. Moreover, for each measurement, only a few computation need to be done.

Recursive Time-Average

This is a better way to compute average of a large measurement sequence. You don't need to store all the measurement data. All you need is to compute the current average is the current measurement data and the previous average . The formula is as follow

(3)

Since the subscript start at 1, then is undefined. For convenient, we can put zero (or any number) to give the correct answer.

Using the previous measurement data of 4, 6, 12, 9 we can get exactly the same result of average as the usual computation method, but in more efficient way. Table below show the computation using the recursive average.

Proof

The development and inductive proof of above formula (3) is as follow:

For :

For :

For :

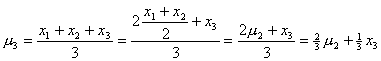
For :

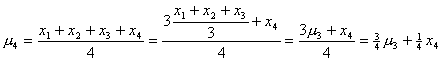
For :

For :

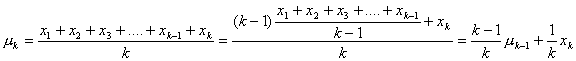(proved)

Characteristics of Time Average

To show the characteristics of time-average, we create random measurement data and plot the data together with the moving average 5 and 10 consecutive data and the time average.

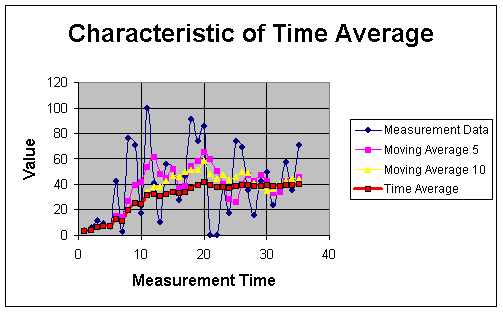
In the graph above, the measurement data was fluctuated randomly from zero to 100. Higher number of data to be averaged make the moving average goes smoother. Time average, however, is the smoothest moving average. It goes directly to the core of the data and lazy to move away from there. As the data fluctuated very much, the moving average will follow the data fluctuation. The time average, however, do not easily deviate away by the fluctuation of the data.

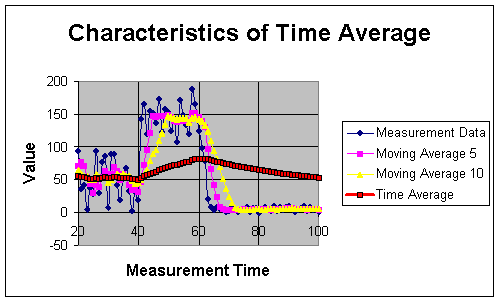
In above graph, we change the measurement data. From measurement time 20 to 40, the data is random between 0 to 100; from measurement time 40 to 60, the data value is randomly fluctuated� between 100 to 200 and above 60, the data is random between 0 to 10.� As usual the moving average will smooth the data while following the fluctuation of� the measurement data. The time average, however, is about the average of the data (around 50) between measurement time 20 to 40. When the measurement move away suddenly above 100, the time average follow to increase with a very slow performance due to long history. Unfortunately, before the time average can reach the average of the data, the measurement data has change again to a very small (below 10). The time average again follow to decrease with a very slow change. Thus, the time average has a long term memory.

Recursive Time-Variance

To compute variance of a large measurement sequence data, recursive time-variance formula (4) below give more efficient computation and data storage. You don?t need to keep all the measurement data. All you need is to compute the current variance is the current measurement data , current time-average and the previous variance . The formula is as follow

(4)

For time , it is defined that . Thus, the computation using equation (4) starts at .

Using the previous measurement data of 4, 6, 12, 9 we can get exactly the same result of variance as the usual computation method, but in more efficient way. Table below show the example of computation using the recursive time-variance formula above.

Proof

The usual way to compute time-variance is given by equation (2). I put here again for your convenient:

(2)

Changing to makes equation (2) becomes

or

(a)

Putting out the last term from equation (2) gives

(b)

Equation (3) can be rearrange into

(c)

The second term of� right hand side of equation (b) can be manipulated as

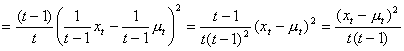
Put back the second term into equation (b) and replace the third term with equation (a) becomes

(proved)

Data Revival from the Statistics

In the previous example, we have the following results:

Suppose we only stored all the time-average data. Can we get back the real measurement data only based on the stored time-average? Yes, we can revive the measurement data only based on the time-average, provided we know the sequence data number .

Remember that we have recursive formula (3) to compute the time-average. I write it again in here for your convenient:

(3)

Rearrange the equation (3) for we have

(5)

As before, the subscript start at 1, therefore is undefined and we can put any number for it. Using equation (5) we can compute back the measurement data based only on two consecutive time-averages.

To restore data from the statistics using equation (5) above, we need to know the sequence data number . Suppose we do not know the sequence data number but we only know time average and time variance of the data, can we revive the real measurement? Yes, we can revive the real measurement data from two consecutive time average and time variance using the following formula

(6)

where,

Using previous example, we have the statistics (time average and time variance) and we can revive the data. Obviously, we use quadratic formula to get the data, thus two possible value are the results.

Note that the only first measurement data is revived using positive sign of equation (6), while the others revival measurement data are obtained using the negative sign. This rule is true for any measurement data.

Proof

I write again equation (5) for your convenient:

(5)

We can rearrange equation (5) to give :

, or

(a)

Preparing for other terms:

(b)

(c)

I write again equation (4) in here:

(4)

Putting equation (b) and (c) into equation (4) gives

(d)

We want to get the value of from equation (d). For this purpose we arrange equation (d) so that it will give a quadratic equation in .

Rearrange for :

(e)

The discriminant of the quadratic equation is