Mahalanobis Distance

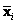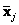Mahalanobis distance is also called quadratic distance . It measures the separation of two groups of objects. Suppose we have two groups with means and , Mahalanobis distance is given by the following

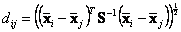
Formula mahalanobis distance

The data of the two groups must have the same number of variables (the same number of columns) but not necessarily to have the same number of data (each group may have different number of rows).

In Matlab, the code is as follow:
function d=MahalanobisDistance(A, B)
% Return mahalanobis distance of two data matrices
% A and B (row = object, column = feature)
% @author: Kardi Teknomo
% http://people.revoledu.com/kardi/index.html
[n1, k1]=size(A);
[n2, k2]=size(B);
n=n1+n2;
if(k1~=k2)
disp('number of columns of A and B must be the same')
else
xDiff=mean(A)-mean(B); % mean diff row vector
cA=Covariance(A);
cB=Covariance(B);
pC=n1/n*cA+n2/n*cB; % pooled covariance matrix
d=sqrt(xDiff*inv(pC)*xDiff'); % mahalanobis distance
end

The code above requires computation of Covariance matrix, which code is given below
function C=Covariance(X)
% Return covariance given data matrix X (row = object, column = feature)
% @author: Kardi Teknomo
% http://people.revoledu.com/kardi/index.html
[n,k]=size(X);
Xc=X-repmat(mean(X),n,1); % centered data
C=Xc'*Xc/n; % covariance

Example

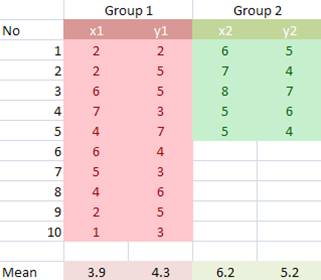
Suppose we have two groups of data, each of group consists of two variables (x, y). The scattered plot of data is shown below. data and mean

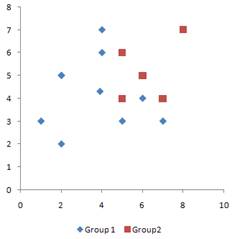
First, we center the data on the arithmetic mean of each variable.

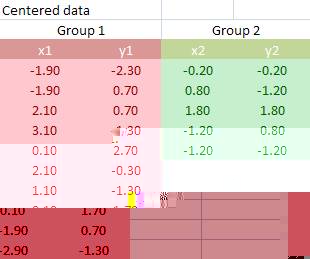
centered data for Mahalanobis distance

Covariance matrix of group 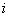Index of group for Mahalanobis distance is computed using centered data matrix

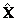
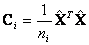
Covariance matrix for Mahalanobis distance

It produces covariance matrices for group 1 and 2 as follow

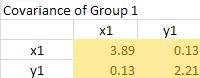
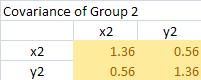
Covariance group 2 Covariance group 1

The pooled covariance matrix of the two groups is computed as weighted average of the covariance matrices. The weighted average takes this form

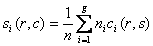Mahalanobis distance .

The pooled covariance is computed using weighted average (10/15)*Covariance group 1 + (5/15)*Covariance group 2 yields

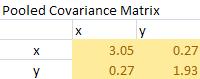
Pooled covariance matrix

The Mahalanobis distance is simply quadratic multiplication of mean difference and inverse of pooled covariance matrix.

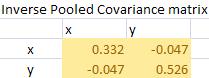
Inverse pooled covariance for Mahalanobis distance Men differences for Mahalanobis distance

To perform the quadratic multiplication, check again the formula of Mahalanobis distance above. When you get mean difference, transpose it, and multiply it by inverse pooled covariance. After that, multiply the result with the mean difference again and you take the square root. The final result of Mahalanobis distance is

Spreadsheet example (MS Excel) of this Mahalanobis computation can be downloaded here .

Use the interactive program below to compute Mahalanobis distance. If you like this program, please recommend it to your friends.

How to use the program:

Input are two matrices name matrix A and matrix B that represent features coordinates of two objects. The columns indicate the features, and the rows are the observations. The number of features of the two objects must be equal (i.e. columns of matrix A = columns of matrix B). Each matrix should have at least 2 rows and 1 column.

A matrix is sequence of numbers in a tabular format, inputted using the following format:

each number in a row is separated by a comma or a space
each row is separated by semicolon ;

Validate your input before running the program. The initial input values are the example.
Refresh your browser to get back the example.

This program is presented by Kardi Teknomo

Samples of Applications of Mahalanobis Distance

Mahalanobis distances in habitat selection studies
Mahalanobis distance for skin color range for face detection
Mahalanobis Distance for Leadership and Education Science
Mahalanobis distance in robotic

< Previous | Next | Content >

Rate this tutorial

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi (2019) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity