Archimedian Double Mean Process

By Kardi Teknomo, PhD .

< Previous | Next | Contents >

Archimedian Double Mean Process

We can view double mean as a general process to find means of two input numbers using as a recurrence formula of two means.

Philips (2000) suggests Archimedean double mean process as a difference equation that involves two means and with two inputs and , which relates to each other using the following formula

Where

Compare this difference equation formula with Gaussian Double mean process .

The Archimedean double mean process has a very nice property that the sequence and will converge to a common limit with linear convergence rate. However, the common limit is not necessarily produce means. For example, if we use arithmetic and geometric mean respectively, we will get which is not means or average.

Example: (Archimedean harmonic-geometric mean)

We use harmonic mean and geometric mean

and

Then the sequence and will converge to a common limit

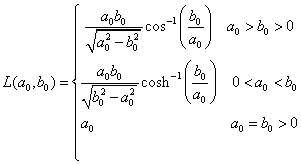
For instance:

, ,

,

Notice that this Archimedean harmonic-geometric mean is not symmetric mean, because in general, .

Note that

< Previous | Next | Contents >

See also: Gaussian Double Mean Process
Rate this tutorial or give your comments about this tutorial

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi (2015) Mean and Average. https:\\people.revoledu.com\kardi\tutorial\BasicMath\Average\