Things you may not know about Factorial Function
Factorial function n! is a multiplication of natural number (positive integer, whole number) up to n.
0! is defined = 1
1! is equal to 1
2! = 1 x 2 = 2
3! = 1 x 2 x 3 = 2 x 3 = 6
4! = 1 x 2 x 3 x 4 = 6 x 4 = 24
5! = 1 x 2 x 3 x 4 x 5 = 24 x 5 = 120
6! = 1 x 2 x 3 x 4 x 5 x 6 = 120 x 6 = 720
7! = 1 x 2 x 3 x 4 x 5 x 6 x 7 = 720 x 7 = 5,040
8! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 = 5040 x 8 = 40,320
9! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 = 40,320 x 9 = 362,880
10! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 10 = 362,880 x 10 = 3,628,800
Interesting things you may not know about Factorial Function
- You see that we can have a recurrence relation n! = n (n-1)!
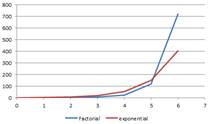
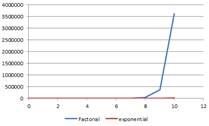
- n-factorial increase rapidly as n goes higher. Factorial function increase more rapidly than exponential function. When n < 6 exponential function produces higher value than factorial function. Starting from n = 6 and above, factorial function is higher and much higher than exponential function. The right figure below that exponential function becomes insignificant compare to factorial when n is equal or larger than 10.
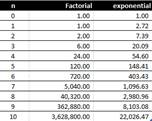
- In most programming languages, there is a limit on our computer in computing factorial function. IEEE double precision value can compute up to 170! When you try to compute 171! it is overflow. The following figure is computation of factorial in Microsoft Excel (using =FACT(n) function).
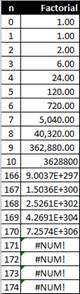
- Factorial up to 22! has exact double precision representation (52 bits of mantissa, not including powers of 2 that are absorbed by the exponent). 23! and above are represented only by approximation.
-
Stirling's Formula approximate factorial function for large n.

The ratio of left hand side and right hand side approach 1 as n approach infinity

We can have variant of Stirling's formula

The probability distribution function (pdf) of standard normal distribution N(0,1) is

Then we can get the total area under the pdf is

Thus, you can see above the connection between Stirling's Formula approximate factorial function and probability distribution function of standard normal distribution
-
Another way to compute factorial is to use Gamma function.

The Gamma function is defined by the integral

There is also recurrence relation of Gamma function

Which is very similar to recurrence relation of factorial function
Lanczos algorithm approximates the computation of Gamma function numerically and this algorithm is useful to compute factorial function numerically.
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2014) Factorial Function.
http://people.revoledu.com/kardi/tutorial/Function/Factorial.htm
