What is Continued Fraction?
Continued fraction is nested fraction or a sequence of fraction. The following expression is called continued fraction
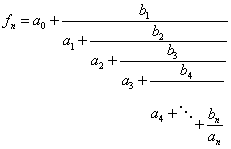
It forms two series of numbers
and
. If the sequence
all become 1, we have what is called
Regular Continued Fraction
, written as
The number
is called the
approximant
or
the
convergence
of continued fraction. The variables in the series
are natural numbers, which sometimes called
element
or
term
. For infinite continued fraction, the approximant will converge to a limit convergence value
. Note however that convergence to infinity
is also acceptable.
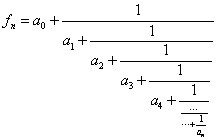
To save space, we usually use the following line notation to express continued fraction
The condense notation of regular continued fraction is
. Personally, I prefer this condense notation as long as it is clear that nominator is always one (i.e. regular continued fraction). When we use a continued fraction but the nominators are not necessarily one (i.e. non-regular continued fraction), in this case, we should use line notation as the most condense notation.
In this tutorial, we will focus only to regular continued fraction, which have 1 as nominators.
Example
: (how to read the condense notation)
,
,
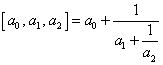
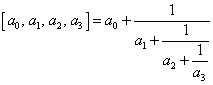
This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Continued Fraction. http://people.revoledu.com/kardi/tutorial/ContinuedFraction/index.html