Rank Reversal

In this simple tutorial I will show that rank aggregation will lead to rank reversal compared to score aggregation.

Suppose 5 judges have to evaluate 10 types of items. Each judge gives score 1 to 100 for each item. Here is an example of their judgments.

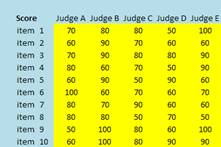
Since all judges are considered equally experts, their weights are equal. Thus, we can either sum their scores or take average of their scores. Our goal in evaluating the items is to rank the items. Table below show the aggregation results and we rank the average (or the sum) of the scores.

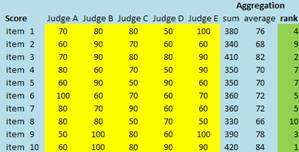
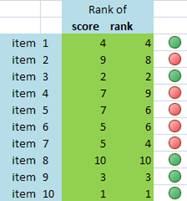
Now suppose we have another scenario that the judges want to use their rank instead of their scores. In this case, each judge will rank their scores. Below are their ranks based on the scores above.

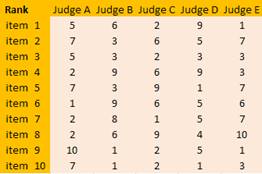
To aggregate the rank, they use the same way as aggregating the scores that is using sum or average. However, this time, we aggregate the ranks instead of the scores. Then, they sort the rank aggregation using based on minimum rank aggregation.

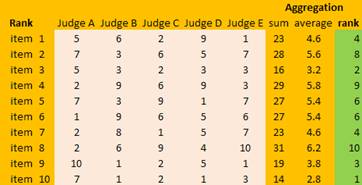
Notice that the rank based on the aggregation of scores is not the same as the rank based on the aggregation of rank. Some item will have reverse order. That is what we called as rank reversal . In general, rank reversal is the rule of rank aggregation. The similarity between rank of scores and rank of rank is just incidental. In the example above, item 2 suppose to have rank 9 but using rank aggregation, it becomes rank 8. On the other hand, item 4 suppose to have rank 7 but using rank aggregation, now it goes down to rank 9.

The simple lesson is: for group decision, use score aggregation, and not rank aggregation because it may lead to rank reversal.

With only $4.99, you will get the more complete e-book of this rank reversal tutorial. Click here to purchase it NOW!
Rate this tutorial

See Also: AHP , Multi Criteria Decision Making

This tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi. (2009) Rank Reversal. http://people.revoledu.com/kardi/tutorial/DecisionAnalysis/Rank-Reversal.htm