<
Previous
|
Next
|
Contents
>
Numerical Example of Affine Difference Equation
We have difference equation y(k+1) = 2 y(k) 5, what is the solution for initial value y(0) = 1 and what is the equilibrium value? How is the stability of this equilibrium value?
Solution
k = 0: y(0) = 1 initial value
k = 1: y(1) = 2 y(0) 5 = -3
k = 2: y(2) = 2 y(1) 5 = -11
= 2 ( 2 y(0)) 5) 5 = 4 y(0) -15
k = 3: y(3) = 2 y(2) 5 = -27
= 2 (4 y(0) -15) 5 = 8 y(0) -35
and so on. For big k value, it is easier to use the
Closed-form Solution
Rather than recursive calculation:
a = 2, b = - 5, k = 10 then
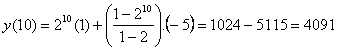
Equilibrium Value
or
If
= 5 then y(k) = 2*5 - 5 = 5 forever. It remain constant at 5 regardless whatever the value of k.
Difference equation y(k+1) = 2 y(k) 5 has solution of
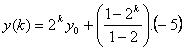and equilibrium value of
.
Stability:
Since a = 2 > 1, the equilibrium is unstable. If the initial value y(0) is smaller than the equilibrium value, the graph of y(k) versus k is exponentially decreasing without bound. If the initial value of y(0) is bigger than the equilibrium value, the graph is exponentially increasing without bound.
<
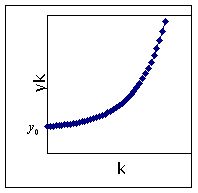
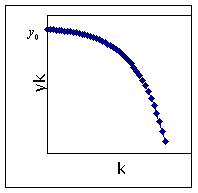
Previous
|
Next
|
Contents
>
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Difference Equation Tutorial. https:\\people.revoledu.com\kardi\ tutorial\DifferenceEquation\