Proof of equation B

By Kardi Teknomo, PhD .

< Previous | Next | Contents >


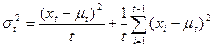
proof of equation b in recursive variance

become

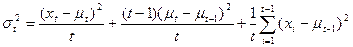proof of equation b in recursive variance (b)

Question: How can it be?

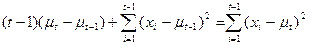
Proof that proof of equation b in recursive variance

Equivalent to

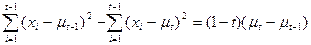proof of equation b in recursive variance (change position of term)

Equivalent to

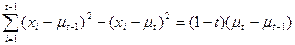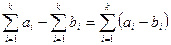proof of equation b in recursive variance (because proof of equation b in recursive variance )

Equivalent to

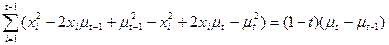proof of equation b in recursive variance (expanding the term of lhs)

Equivalent to

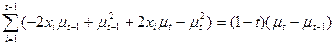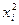proof of equation b in recursive variance (cancel out proof of equation b in recursive variance )

Equivalent to

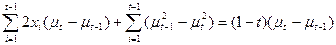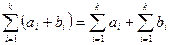proof of equation b in recursive variance (because proof of equation b in recursive variance )

Equivalent to

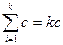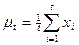proof of equation b in recursive variance (because proof of equation b in recursive variance )

Since

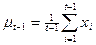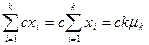
proof of equation b in recursive variance and proof of equation b in recursive variance then proof of equation b in recursive variance

Then it is equivalent to

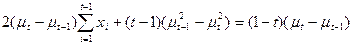
proof of equation b in recursive variance

or

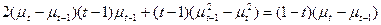
proof of equation b in recursive variance

Remove t-1 term and put rhs to the left become

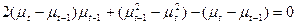
proof of equation b in recursive variance

or

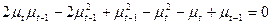
proof of equation b in recursive variance

or

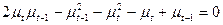
proof of equation b in recursive variance


See Also: proof of recursive variance formula

< Previous | Next | Contents >

These tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi. (2006) Recursive Average and Variance.
http://people.revoledu.com/kardi/tutorial/RecursiveStatistic/index.html