<
Previous
|
Next
|
Contents
>
Read this tutorial comfortably off-line. Click here to purchase the complete E-book of this tutorial
Solutions of the Tower of Hanoi
In this section, you will learn the solution of the Tower of Hanoi using Q-Learning. Click here if you want to actually play this game
To use Q learning to solve this problem, I transform the solution space graph in previous page into state-diagram with reward value of zero to all links except the direct link heading to the goal and the loop in the goal. See the state diagram below.
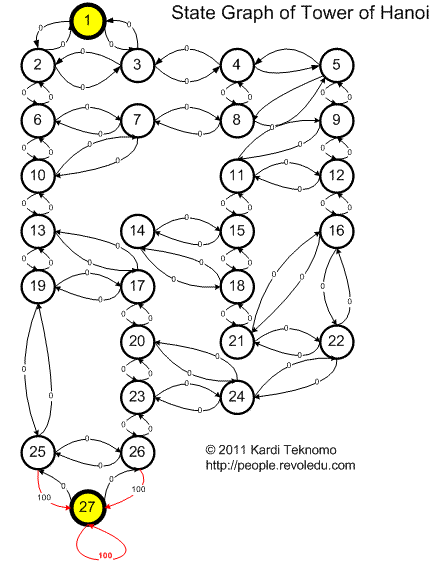
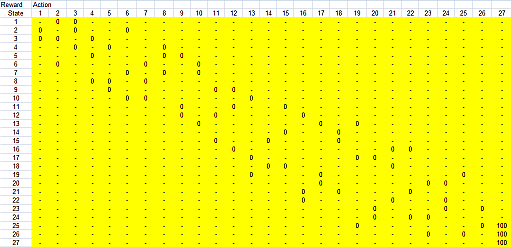
To solve this problem, we transform the state diagram above into R matrix as shown in the picture below (I used MS Excel without any programming, you can download the MS Excel file here ).
Remember the R matrix is simply an adjacency matrix of the state graph above, with special attention to the links toward the goal. All links toward the goal (including an additional self loop) must have high value (100) while all other links have zero values. Non-connected nodes are not considered, and therefore the value is infinity.
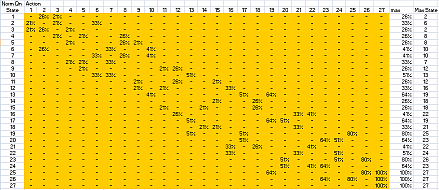
Then transform the R matrix into Q matrix and normalized it. Do you still remember, how to transform R matrix into Q matrix? Read back the Q-learning tutorial .
The result of normalized Q matrix is given below. These values can then put back into the state graph to get the solution.
You can also see the solution in the state diagram below. The red color of arrow is the optimum path (minimum path) from initial state to the goal state.
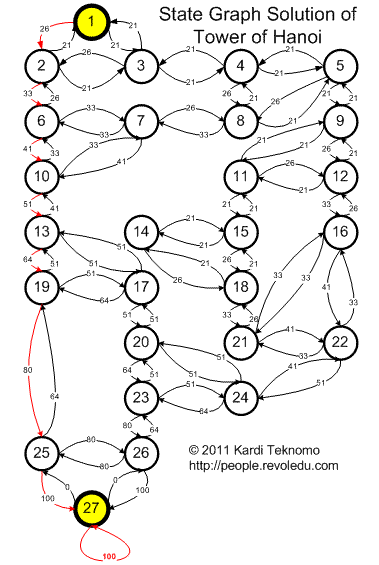
Actually, the Q values in this diagram will lead to any initial state (not only from state 1) to the goal state using minimum path. Very impression solution, isn't it?
To go from any state to the goal state, the agent only need to maximize the value of the arrow out of that state. Following these simple maximization procedures will eventually get the optimum solution! Q-Learning has transformed the global navigational values into local decision by the agent. In my scientific papers, I called these kinds of transformations as Sink Propagation Values (SPV).
So, what is the solution of the tower of Hanoi?
The results is given as sequence of states is shown in the figure below
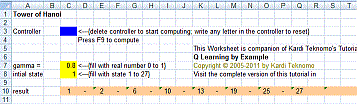
Better yet, graphical solution is always the best. Just follow the red arrow, you will get the optimum solution.

As summary, Q-Learning can help agent navigation and path motion planning such that the agent can find the optimum solution from any state to the goal state. Unless Dikjstra or A* method that find the optimum solution between two pairs of node, Q-learning will solve the optimum solution from any nodes to the goal node.
< Previous | Next | Contents >
Preferable reference for this tutorial is
Teknomo, Kardi. 2005. Q-Learning by Examples. http://people.revoledu.com/kardi/tutorial/ReinforcementLearning/index.html

