What is SVM?
In short, Support Vector Machine (SVM) is a supervised learning algorithm that classifies both linear and nonlinear data based on maximizing margin between support points and a nonlinear mapping to transform the original training data into a higher dimension.
In this tutorial, I will teach you SVM in a very gentle way. We will learn something more difficult such as solving linearly non-separable case later. A first, you should learn something easier: linearly separable case. Once you master the technique for linearly separable case, going further for more general linearly non-separable case as well as the kernel tricks would be just additional easy steps for you.
You have learned what the meaning of supervised learning in the previous section. In this section, I will explain the meaning of SVM intuitively without mathematics. By the end of this section, you should know what is margin and support points and why do we need to maximize the margin.
Let us start with a linearly separable case. I have shown the picture on the left below in the last section. The classes in the training data can be separated by a decision line. A decision line is a boundary to separate classes in the training data. For the same training data, we can draw many decision lines to separate the training data. Does this decision line characterize the optimum line to separate the classes in the training data? Which line is the best decision line? If you observe more carefully, you will find that none of the line in the three charts below is the best decision line (why?). In later section of this tutorial, you will find the decision line of this training data with numerical example.
 .
.
 .
.
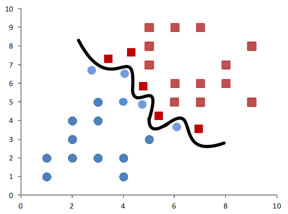
Let me show you another set of training data. This training data is also linearly separable data. Instead of drawing a line to separate the training data, now I draw several decision lines. Each of these decision lines can be used to separate the training data. Which line is the best decision line? Why do we call it the best decision line?

A line to separate the training data is the best decision line if we do not need to change that decision line when a new instance of data come in as part of our training data. If the additional new instance data is not robust enough to be predicted correctly, our decision line is probably no so useful. In fact, we can use irregular decision line rather than a straight decision line to over fit the training data like the figure below but this kind of model is pretty useless for prediction. Our purpose in modeling our data using SVM is to predict the classification of the new instance data correctly. The irregular decision line below is an over-fitting model that it it is only good to fit your training data but it is not good for prediction.
Since we do not know if the new data will change the decision line or not, all we can do is to minimize the risk to change the decision line. Let me explain this risk minimization in more intuitive way. To minimize the risk of changing the decision line, naturally it is a good idea to find a decision line that pass through the middle of the data. Using the same training data, now I can draw a decision line that separate the training data in the middle.
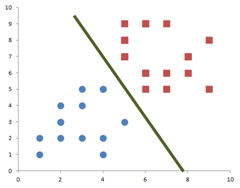
At the same time, I also have found that probably this red decision line in the following picture below might also be a candidate for the best decision line because it is also passed in the middle of the training data. Among the two decision lines below, green line and red line, which do you think is the better decision line? Why?
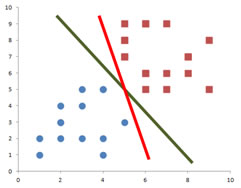
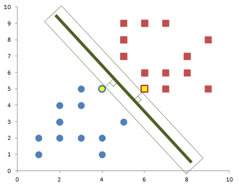
What I will do is to expand each decision line until it reaches the first data points. Comparing the expansion of the green decision line and the expansion of the red decision line, which do you think is the best decision line? Since the green decision line produces wider expansion than the red decision line, we can say that the chance of the green decision line to change due to adding new instance of data is smaller than the red decision line. We call the width of rectangle expansion of the middle line as a margin . Margin is the smallest distance the decision line and any training data. Thus, the best decision line is the line that produces the widest margin. In other words, we need to find the optimum solution by maximizing the margin.
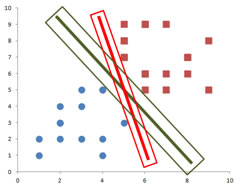
If you look at the green decision line and its margin into more detail, we can see that the margin of the decision line actually touches several data points from both classes in perpendicular way.
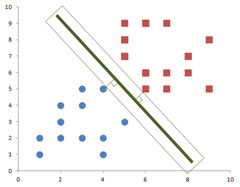
The data points that are touched by the margin are special because they are the one which determine the margin and the decision line itself. Therefore, we give special name to these data points. They are called support vectors or support points .
Do you have question regarding this SVM tutorial? Ask your question here !

