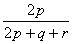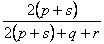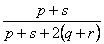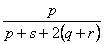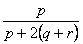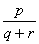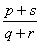Distance for Binary Variables
We often face variables that only binary value such as Yes and No, or Agree and Disagree, True and False, Success and Failure, 0 and 1, Absence or Present, Positive and Negative, etc. For such binary variables, there are only two possible values, which can be represented as positive and negative. Similarity of dissimilarity (distance) of two objects that represented by binary variables can be measured in term of number of occurrence (frequency) of positive and negative in each object.
For example:
|
Feature of Fruit |
Sphere shape |
Sweet |
Sour |
Crunchy |
|
Object
|
Yes |
Yes |
Yes |
Yes |
|
Object
|
No |
Yes |
No |
No |
The coordinate of Apple is (1,1,1,1) and coordinate of Banana is (0,1,0,0). Because each object is represented by 4 variables, we say that these objects has 4 dimensions.
Let
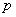 = number of variables that positive for both objects
= number of variables that positive for both objects
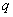 = number of variables that positive for the
= number of variables that positive for the
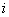 th objects and negative for the
th objects and negative for the
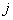 th object
th object
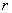 = number of variables that negative for the
= number of variables that negative for the
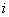 th objects and positive for the
th objects and positive for the
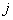 th object
th object
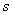 = number of variables that negative for both objects
= number of variables that negative for both objects
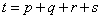 = total number of variables
= total number of variables
Object
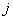
|
|||
| Yes | No | ||
object
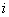
|
Yes |
|
|
|
|
No |
|
|
For our example above, we have measured Apple and Banana have
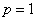 ,
,
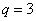 and
and
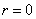 ,
,
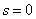 . Thus,
. Thus,
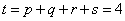
The most common use of binary dissimilarity (distance) is
B.S. Everit (1978) listed 10 other similarity measures for presence-absence data that have been proposed
This tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity


 =Apple
=Apple
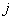 =Banana
=Banana
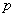
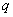
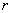
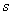
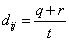
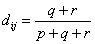
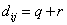
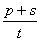 =
=
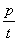
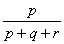 =
=