Share this:
Google+
< Previous | Contents | Next >
How to know the probability distribution of a random walk?
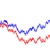
Suppose you have a given a random walk model in the black box. You want to know what the underlying distribution that generate this random walk model. Say, you want to know what is the probability distribution of the particle at t=100? Thus, you are recording the location X(100) and generate such X(100) thousands of times.
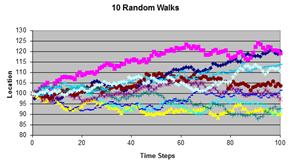
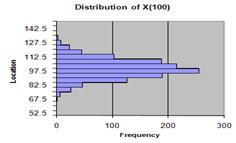
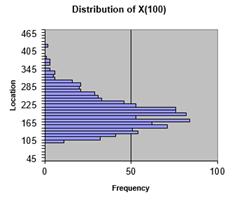
How to recognize that a time series data was generated based on random walk of Normal Distribution? Suppose we generate the random walk N=10,000 times and we record only at certain time, say t=100. Now if we plot the distribution of \( x_{100} \) would be approximately similar to the underlying distribution that creates the random walk.

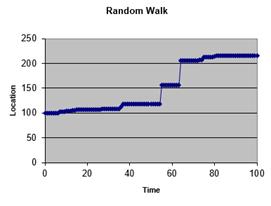
Now suppose we use another probability distribution. Say, we want to use Poisson noise instead of Gaussian noise. We know from statistics that the inverse of Poisson distribution is an exponential distribution. Thus, to generate the Poisson noise say at average of \( \lambda=60 \) we use
$$ \Delta x_t = x_{t+1} - x{t} = EXPONDIST(U,\lambda, 0) $$
The random walk plot is now similar to an increasing stair case and the probability distribution of \( x_{100} \) is now asymmetric similar to the underlying distribution that creates the random walk.
< Previous | Contents | Next >
Do you have question regarding this Stochastic Process tutorial? Ask your question here
These tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. (2019) Stochastic Process Tutorial .
http://people.revoledu.com/kardi/tutorial/StochasticProcess/