How the K-Mean Clustering algorithm works?

KMean e-book

< Previous | Next | Contents >

K Means Algorithm

Read this tutorial off-line from any device! Purchase the complete e-book of this k means clustering tutorial here .

This part of tutorial describe the algorithm of k-mean clustering. To understand what is k-means clustering, click here . Get the PDF copy of this k means clustering tutorial here

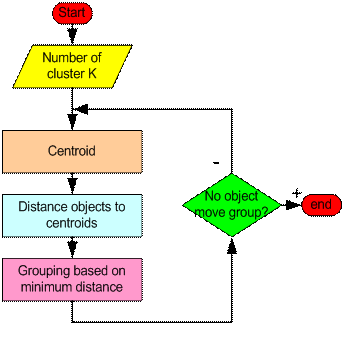
Here is step by step k means clustering algorithm:

K means clustering algorithm

Step 1 . Begin with a decision on the value of k = number of clusters

Step 2 . Put any initial partition that classifies the data into k clusters. You may assign the training samples randomly, or systematically as the following:

  1. Take the first k training sample as single-element clusters
  2. Assign each of the remaining (N-k) training sample to the cluster with the nearest centroid. After each assignment, recomputed the centroid of the gaining cluster.

Step 3 . Take each sample in sequence and compute its distance from the centroid of each of the clusters. If a sample is not currently in the cluster with the closest centroid, switch this sample to that cluster and update the centroid of the cluster gaining the new sample and the cluster losing the sample.

Step 4 . Repeat step 3 until convergence is achieved, that is until a pass through the training sample causes no new assignments.

If the number of data is less than the number of cluster then we assign each data as the centroid of the cluster. Each centroid will have a cluster number. If the number of data is bigger than the number of cluster, for each data, we calculate the distance to all centroid and get the minimum distance. This data is said belong to the cluster that has minimum distance from this data.

Click here to see how this k-means algorithm algorithm is implemented in code or if you prefer numerical example (manual calculation) you may click here.

Since we are not sure about the location of the centroid, we need to adjust the centroid location based on the current updated data. Then we assign all the data to this new centroid. This process is repeated until no data is moving to another cluster anymore. Mathematically this loop can be proved to be convergent. The convergence will always occur if the following condition satisfied:

  1. Each switch in step 2 the sum of distances from each training sample to that training sample's group centroid is decreased.
  2. There are only finitely many partitions of the training examples into k clusters.

Read this tutorial off-line from any device! Purchase the complete e-book of this k means clustering tutorial here .


Do you have question regarding this k means tutorial? Ask your question here

< Previous | Next | Contents >