What is boostsrap sampling?
Bootstrap is sampling with replacement from a sample. Bootstrap is sampling within a sample. The name may come from phrase "pull up by your own bootstraps" which mean "rely on your own resources". Bootstrap sampling relies on its own sample as often the only resources a researcher has. Bootstrap correspondence principle says that estimator of sub sampling (taken by bootstrap method) is equal to the estimate of sample.
The idea of bootstrap is shown in the diagram above. Suppose you want to assess statistical accuracy of your sample data (statistics of sample), you can take N bootstrap samplings (sometimes its called bootstrap resampling) and compute the statistics from each boostrap sampling. The values of boostrap statistics are used to evaluate the statistical accuracy of the origial sample statistics.
Click here on example of how to do bootstrap sampling
What are the assumption of Bootstrap?
Bootstrap method has assumption
- Your sample is a valid representative of the population
- Bootstrap method will take sampling with replacement from the sample. Each sub sampling is independent and identical distribution (i.i.d.). In other word, it assumes that the sub samples come from the same distribution of the population, but each sample is drawn independently from the other samples.
Example Applications of Bootstrap
Here are some typical statistical examples of problems that you can use Bootstrap method to solve
- Suppose you have some sample data but your sample is quite small that you are not sure the population theoretical distribution of your sample. How could you estimate the inter quartile range (IQR) or variance of the mean average of your sample?
- You have two samples from unknown distribution, name them X and Y. You want to know the distribution of ratio Z = X/Y and want to derive some useful statistics (such as mean and standard deviation) from the distribution of the ratio.
- You have two samples A and B and you want to test whether they come from the same population
-
You have regression model
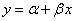and you want to get the confidence interval of the parameters
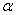and
.
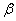This tutorial is copyrighted .
Preferable reference for this tutorial is
Teknomo, Kardi. Bootstrap Sampling Tutorial. http://people.revoledu.com/kardi/tutorial/Bootstrap/