<
Previous
|
Next
|
Contents
>
Difference Equation
Dynamical system come with many different names. Our particular interesting dynamical system is for the system whose state depends on the input history. In discrete time system, we call such system difference equation (equivalent to differential equation in continuous time).
Difference equation is an equation involving differences. We can see difference equation from at least three points of views: as sequence of number, discrete dynamical system and iterated function. It is the same thing but we look at different angle.
- Difference equation is a sequence of numbers that generated recursively using a rule to relate each number in the sequence to previous numbers in the sequence.
Example:
-
Sequence
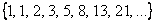is called Fibonacci sequence, generated with rule
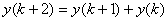for
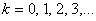and initial value
-
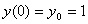
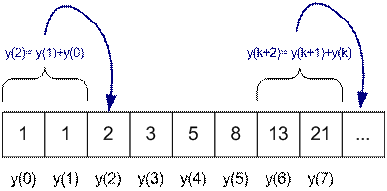
Sequence
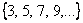has rule
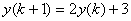for
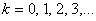. Both sequences have initial value of
.
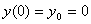- Difference equation is a discrete dynamical system that take some discrete input signal and produce output signal
Example:
-
Dynamical system
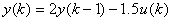take unit step input
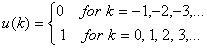will produce output of
-
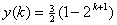
Difference equation is an
iterated map
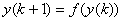if we see the sequence as an
iterated function
:
,
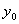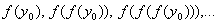The
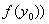is the first iterate of
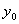under
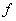. Notation
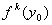is the k-th iterate of
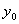under
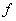. For example,
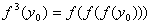. The set of all iterates of
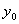is called the
orbit
of
.
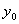Example:
Iterated function
for
= 1 will produce orbit
. If
= 2, the iterated function generate
. When
= 0.5, the iterated function yield sequence of
We see that knowing the rule only is not enough to know the behavior
of the sequence. Initial value is also very important. The orbit of
= 1 is constant for function
while for
= 2 produces unbounded orbit and the orbit is attracted to zero for
= 0.5. The figure below show the orbit of
= 0.5. We will discuss the meaning of this kind of figure later in Phase
Diagram.
Knowing the initial value and the rule, we can generate
the whole sequence recursively. The value of
is an integer (
) and the rule to generate the sequence is called the
difference
equation
or the
dynamical system
or
iterated function.
See Also: Index and Initial Value Agreement
<
Previous
|
Next
|
Contents
>
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Difference Equation Tutorial. https:\\people.revoledu.com\kardi\ tutorial\DifferenceEquation\