EM Algorithm

By Kardi Teknomo, PhD.


Share this: Google+

< Contents | Previous | Next >

What is Expectation-Maximization (EM) algorithm?

Expectation-Maximization (EM) algorithm is an iterative procedure to estimate the maximum likelihood of mixture density distribution. Just to give a note about the name, Baum-Welch Algorithm that are used in Hidden Markov Model (HMM) is a special case of Expectation-Maximization (EM) algorithm.

The original theory of EM algorithm was to obtain mixture probability density distribution from 'incomplete' data samples. Suppose you found out that the distribution of your data is not unimodal and you suspect that the mixture distribution is Gaussian. For simplicity, you suspect there are three components of your Gaussian mixture model. You want to know each of your data is actually belong to which of the three components. If you know which component of the mixture, then you can compute the likelihood of your data. For now, you simply think the likelihood is just a probability index value to represent your model and your data. Later on we will go into more detail computation and the actual meaning.

Now let us imagine there is a hidden variable h to associate which data belong to which component of the mixture. Say, if the data belongs to component number 1. The value of and when if the data belongs to component number 2 and 3 respectively. A data is called complete if we know the value of that hidden variable. Dempster and his friends argued that the mixture distribution can be found using Maximum Likelihood (ML) method, if the data is 'complete'. In reality, however, we actually do not know the value of that hidden variable. Thus, our data is actually 'incomplete'.

To solve the above problem of incomplete data, there is an awesome procedure (or algorithm) that can give you the estimate of the value of the hidden variable and it is also produced the weights and parameters estimation of the Gaussian Mixture model to maximize the likelihood of your data. This algorithm is called EM algorithm.

EM algorithm consists of two steps. The first step is called Expectation (E) step. Next step is called Maximization (M) step. The convergence of the EM algorithm is guaranteed by a theorem proved by Dempster et al (1977).

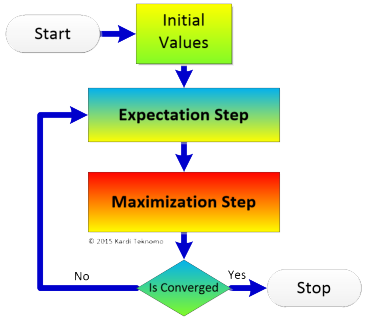
EM Algorithm

In Expectation step, we first compute the expected probability that a component distribution generates that data point. In the Expectation step we guess the value of the hidden variable that we do not know based on the expected probability. Knowing the value of the hidden variable, we can compute the value of log-likelihood of complete data. As the result of our guessing on that hidden variable, our data is now 'complete'.

Next step is called Maximization (M) step. In this Maximization step, the parameters and mixing weight that maximize the expected log-likelihood of complete data are computed. Thus, in the Maximization step, we guess the mixture distribution using maximum likelihood estimation assuming that our complete data is correct.

As we repeat the two steps above iteratively until we will get the estimation of the true value of the expected probability as well as the three parameters of the mixture distribution. When you get the final results of the parameter estimate and the weights of each component, you will at the same time get the maximum likelihood estimation.

EM algorithm can be applied to any type of component density distribution. It is not necessarily Normal distribution. In this tutorial, however, we simplified the problem to apply EM algorithm only for data with assumption on mixture of Normal distribution. (Usually you should prove first that the assumption of Normality is correct). Thus, we will apply EM algorithm for Gaussian Mixture Model.

Summary

As summary, here is what you have learned so far in this section.

  1. In each iteration, EM algorithm consists of two steps: Expectation step and Maximization step
  2. In the Expectation step, you get expected probability of each data to belong to a certain component of the mixture distribution
  3. In the Maximization step, you get the parameter estimation and the weight of each component of the Mixture distribution
  4. The result of EM algorithm is to maximize the likelihood probability of all your data by changing the distribution parameters and weights.
In the next section, you will learn the numerical example of EM algorithm to solve Gaussian Mixture Model .

These tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi. (2019) Gaussian Mixture Model and EM Algorithm in Microsoft Excel.
http://people.revoledu.com/kardi/tutorial/EM/

Reference