Maximum Likelihood

By Kardi Teknomo, PhD.


Share this: Google+

< Contents | Previous | Next >

What is Maximum Likelihood?

Given a probability distribution, you want to estimate the parameters of the distribution. Recall that a Normal distribution has two parameters: mean Maximum Likelihood and variance Maximum Likelihood . Mean is the average of the data which measures the central tendency of the data. Variance is the average of square deviation of the data from the mean.

There are many ways to estimate the parameter of a distribution. One of the most well-known method to estimate the parameter of a distribution is called Maximum Likelihood method as proposed by well -known statistician R. A. Fisher in 1912. The method is to form a likelihood function from the Maximum Likelihood sample data Maximum Likelihood and then take the partial derivative with respect to its parameters and set it to zero. The likelihood function is the product of the probability density function of all sample data.

Maximum Likelihood

Let us take an example of a Normal distribution which probability density function is given as

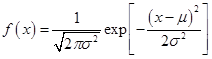
Maximum Likelihood

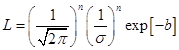For Maximum Likelihood sample data Maximum Likelihood , the likelihood function is

Maximum Likelihood where Maximum Likelihood

Taking the logarithm to the likelihood function gives

Maximum Likelihood

Taking the partial derivative with respect to the mean, we have

Maximum Likelihood Maximum Likelihood Maximum Likelihood

Taking the partial derivative with respect to the standard deviation, we have

Maximum Likelihood Maximum Likelihood Maximum Likelihood

Observed that given a probability density function, we can use calculus to find the formula parameters of the distribution.

For Gaussian Mixture distribution, however, the likelihood function is

Maximum Likelihood

Function Maximum Likelihood produces 1 if the data Maximum Likelihood is belong to component Maximum Likelihood and zero otherwise. The weights of component Maximum Likelihood is Maximum Likelihood . The Normal density function Maximum Likelihood of data Maximum Likelihood is now depends on component Maximum Likelihood . To use calculus to solve the partial derivative is very difficult. A numerical method is needed. Numerical method will not give you the formula of the parameters but it will give you the values of the parameters.

Summary

Let us summarize what you have learned in this section:

  • Maximum Likelihood method is useful to find the parameters of a distribution.
  • For GMM, maximum likelihood method using partial derivative is too difficult. We need numerical solution.

In the next section, you will learn an algorithm to solve GMM numerically .

.

These tutorial is copyrighted .

Preferable reference for this tutorial is

Teknomo, Kardi. (2019) Gaussian Mixture Model and EM Algorithm in Microsoft Excel.
http://people.revoledu.com/kardi/tutorial/EM/