Solving Simultaneously Linear Equations Using Microsoft Excel

by Kardi Teknomo

Share this: Google+

Solving Linear Equation using Excel

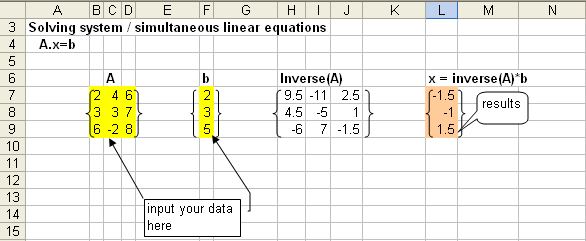
This tutorial will describe how to use an inverse function for matrix in Microsoft Excel to solve non-homogeneous simultaneous linear equations.

The spreadsheet example can be downloaded here .

Suppose we want to solve simultaneous equations below

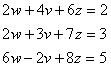
We can convert the simultaneous equations above into matrix form where

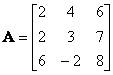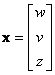, and

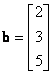
The solution of the simultaneous equations can be easily obtained using inverse matrix

Here is systematically how to do it in Microsoft Excel.

You may download the spreadsheet example here .

1. Input the numbers of matrix 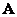and vector
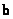
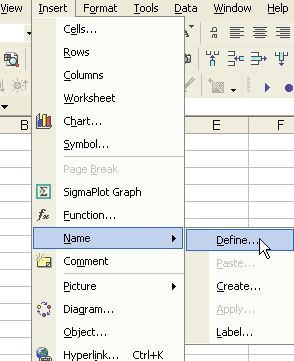
2. Tell MS Excel the name of this matrix by menu Insert-Name-Define .

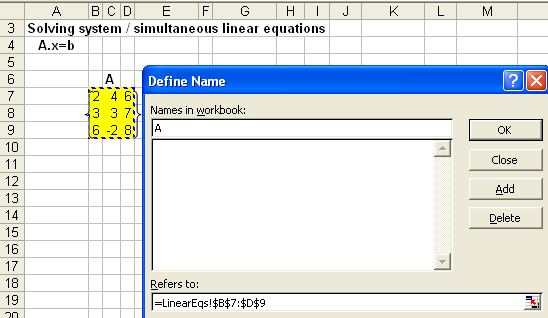
3. A defined-name dialog will appear and type the name of matrix and refer to the range of the matrix , then click OK. In a similar way, you define the name of vector .

4. In a cell where do you want to put the inverse of matrix , you type =MINVERSE( ) . It will give you only one number. Now using the mouse highlight the range where do you want to put the inverse of matrix . Because you know that the size of inverse is also 3 by 3 matrix, highlight only that range. While highlighting, press F2 and then Shift-Ctrl-Enter. You will get the inverse of matrix .

5. Now you define name of inverse matrix and use matrix multiplication function to get the solution. To do that, in the cell where do you want to put the solution, type =MMULT(Inverse_A,b). It will give you only one number. Now using the mouse highlight the range where do you want to put the solution. Because you know that the size of solution is a single column with 3 rows, highlight only that range. While highlighting, press F2 and then Shift-Ctrl-Enter and you will get the solution.

See also:
MS Excel Tutorial index , Kardi Teknomo's Tutorial , Online interactive program to solve simulateneous equations using generalized inverse

Send your comments, questions and suggestions