Adjacency Matrix: Vertex to Vertex
The graph family argues that one of the best ways to represent them into a matrix is by counting the number of edge between two adjacent vertices.
Two vertices is said to be adjacent or neighbor if it support at least one common edge.
Let us start with example
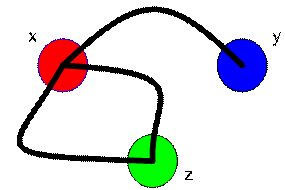
Graph below has three vertices. Thus, we make adjacency matrix of size 3 by 3. Then we put the name of vertices on the side of the matrix. Look at the picture and we start with an empty matrix. Only the names of vertices are there
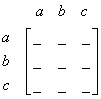
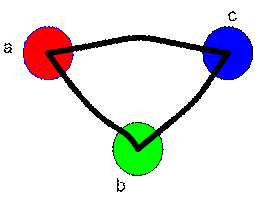
To fill the adjacency matrix, we look at the name of the vertex in row and column. If those vertices are connected by an edge or more, we count number of edges and put this number as matrix element.
Vertex
and vertex
has one common edge, we say that Vertex
and vertex
are adjacent (neighbor). We input the number of edge in the matrix cell that correspond to vertex
and vertex
.
Vertex
and
is adjacent by one edge. Thus, we input the number of edge in the matrix cell that correspond to Vertex
and
.
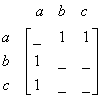
Similarly, vertex
and
is connected by one edge. Thus, we input the number of edge in the matrix cell that correspond to vertex
and
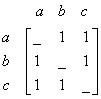
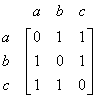
There is no other edge on the graph, thus we put the rest of unfilled cells in the matrix as zero
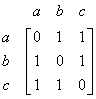
The matrix to represent a graph in this way is called Adjacency matrix .
The size of adjacency matrix is equal to the number of vertices in the graph. It is a square matrix (that is the number of rows is equal to the number of columns).
The adjacency matrix of a graph is symmetric because it has no direction. Two vertices share the same edge can be called from the first one to the second one, or from the second one to the first one. For example, Vertex
and vertex
has one common edge, then element (a, b) = 1 and element (b, a) = 1.
Let us try another example:
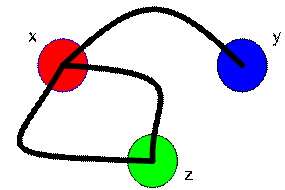
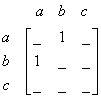
Can you make the adjacency matrix of this graph? Try it first before you look at the answer below.
The graph has 3 vertices, thus we make a matrix size 3 by 3. We put the name of vertices on the side of the matrix.
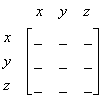
Now look at the vertex
and vertex
. How many edges do the two vertices support? One. Then we put this value into the matrix
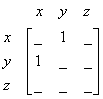
Look at vertex
and vertex
. How many edges do these vertices support? None. Then, we put value zero into the corresponding cell in the matrix
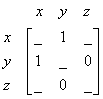
Next, you look at vertex
and vertex
. How many edge these vertices support? Two. Then we input the matrix into
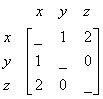
Since there is no other edge in the graph, we can fill the empty cell with zeros. Thus, we have the answer
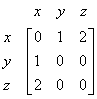
Some of you may ask about the diagonal part of the matrix, are these cells always zero? No, if you find the graph has some loop in some vertices, you can fill the diagonal element of adjacency matrix with the number of loop.
If a graph has some vertex that is not connected to any other vertices, the adjacency matrix correspond to that single vertex is zero.
Please do some practice to represent graph below into adjacency matrix.
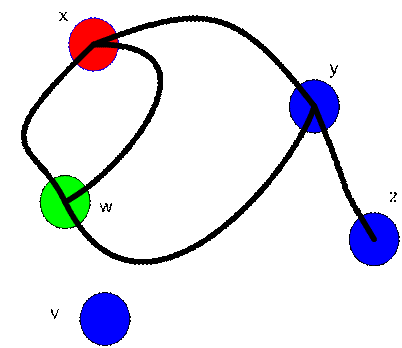
(See the answer in the previous page )
Given the adjacency matrix, can you draw back the graph?
Check example application of graph theory in Q-Learning Tutorial
<
Back
|
Next
|
Content
>
These tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Pictorial Introduction to Graph Theory. https:\\people.revoledu.com\kardi\ tutorial\GraphTheory\