Incidence Matrix: Vertex to Edge
"Where are the edges?" said other graph families who like to point that Adjacency matrix does not distinguish the edges. "The adjacency matrix only counts the number of edges, not distinguish them".
Then, the other graph family state that one of the best ways to represent them into a matrix is by counting the connection between edge and vertices.
Instead of making matrix between vertex and vertex, they want to make matrix that related vertices to edges.
A vertex is said to be incident to an edge if the edge is connected to the vertex.
Let us start with example.
Graph below has three vertices and four edges. Thus, we make incidence matrix of size 3 by 4. The rows represent the vertices; the columns are for the edges. Then we put the name of vertices and edges on the side of the matrix. Look at the picture and we start with an empty matrix. Only the names of vertices are there.
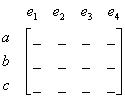
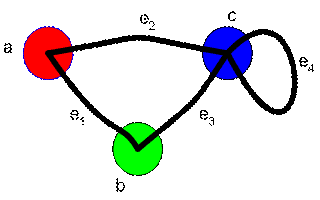
To fill the incidence matrix, we look at the name of the vertex in row and name of the edge in column and find the corresponding of it. If a vertex is connected by an edge, we count number of leg in which the edge is connecting to this vertex and put this number as matrix element.
You can fill the matrix row by row or column by column. For our example, we will fill row by row. Thus, we look at each vertex, and check the edge connecting to that vertex.
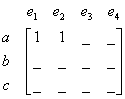
Now look at Vertex
. Edge
and edge
are connected to this vertex, each with one leg on the vertex. Thus, we fill the matrix with these numbers.
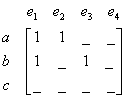
Vertex
connected to edge
and
with one leg each. Then we fill the matrix with these numbers.
Vertex
has connection to three edges
,
and
. Edge
and edge
, each of them has only one leg connected to vertex
. Because edge
is a loop, it has two legs connected to vertex
. We fill the matrix with these numbers.
We have finished considering all vertices. The rest of the unfilled cells in the matrix is filled with zero.
The matrix to represent a graph in this way is called Incidence matrix .
The size of incidence matrix is equal to number of vertices and number of edges. If you notice carefully, you can observe that the sum of each column in incidence matrix is equal to 2, while the sum of each row in incident matrix is equal to the degree or valency of that vertex.
You may remember that degree of a vertex (indicate how honorable the vertex is) is closely related to the number of edge that vertex can support.
If you forget about what is valency or degree , read back the tutorial on that part.
This tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Pictorial Introduction to Graph Theory. https:\\people.revoledu.com\kardi\tutorial\GraphTheory\