How K-Nearest Neighbor (KNN) Algorithm works?

By Kardi Teknomo, PhD.

<Contents | Previous | Next >

K nearest neighbor algorithm is very simple. It works based on minimum distance from the query instance to the training samples to determine the K-nearest neighbors. After we gather K nearest neighbors, we take simple majority of these K-nearest neighbors to be the prediction of the query instance.

The data for KNN algorithm consist of several multivariate attributes name that will be used to classify . The data of KNN can be any measurement scale from ordinal, nominal, to quantitative scale but for the moment let us deal with only quantitative and binary (nominal) . Later in this section, I will explain how to deal with other types of measurement scale.

Suppose we have this data:

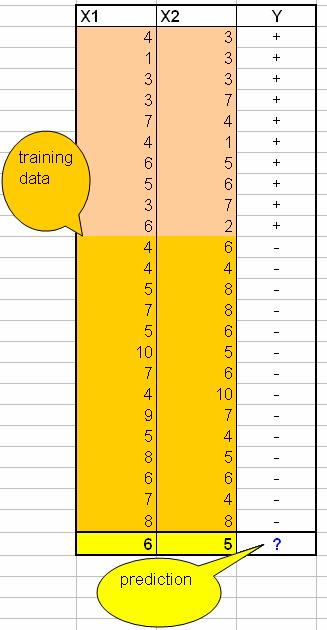
The last row is the query instance that we want to predict.

The graph of this problem is shown in the figure below

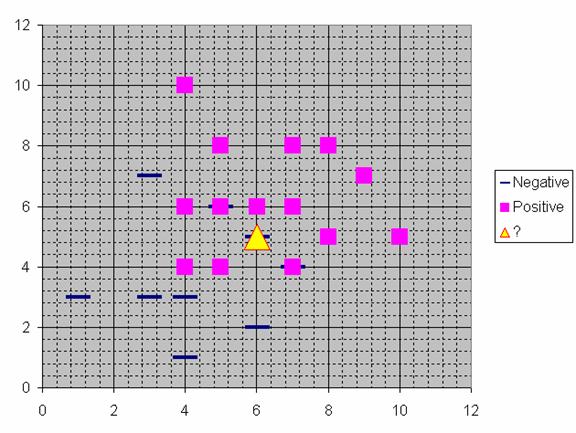
Suppose we determine K = 8 (we will use 8 nearest neighbors) as parameter of this algorithm. Then we calculate the distance between the query-instance and all the training samples. Because we use only quantitative , we can use Euclidean distance. Suppose the query instance have coordinates ( , ) and the coordinate of training sample is ( , ) then square Euclidean distance is . See Euclidean distance tutorial when you have more than two variables. If the contains some categorical data or nominal or ordinal measurement scale, see similarity tutorial on how to compute weighted distance from the multivariate variables.

The next step is to find the K-nearest neighbors. We include a training sample as nearest neighbors if the distance of this training sample to the query instance is less than or equal to the K-th smallest distance. In other words, we sort the distance of all training samples to the query instance and determine the K-th minimum distance.

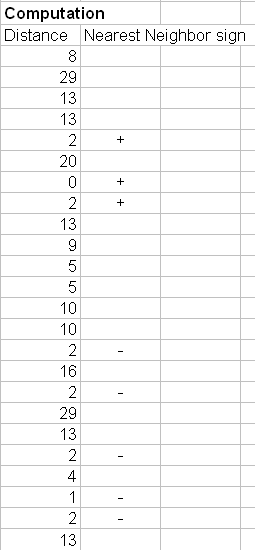
If the distance of the training sample is below the K-th minimum, then we gather the category of this nearest neighbors' training samples. In MS excel, we can use MS Excel function =SMALL(array, K) to determine the K-th minimum value among the array. Some special case happens in our example that the 3 rd until the 8 th minimum distance happen to be the same. In this case we directly use the highest K=8 because choosing arbitrary among the 3 rd until the 8 th nearest neighbors is unstable.

The KNN prediction of the query instance is based on simple majority of the category of nearest neighbors. In our example, the category is only binary, thus the majority can be taken as simple as counting the number of ‘+' and ‘-‘ signs. If the number of plus is greater than minus, we predict the query instance as plus and vice versa. If the number of plus is equal to minus, we can choose arbitrary or determine as one of the plus or minus.

If your training samples contain as categorical data, take simple majority among this data. If the is quantitative, take average or any central tendency or mean value such as median or geometric mean.

Give your comments, questions or suggestions

<Contents | Previous | Next >

This tutorial is copyrighted.

Preferable reference for this tutorial is

Teknomo, Kardi. K-Nearest Neighbors Tutorial. http:\\people.revoledu.com\kardi\ tutorial\KNN\