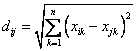Euclidean Distance
Description
Formula
Euclidean Distance Calculator
Numerical Example
Pattern of 2 Dimensional Euclidean Distance
Pseudo Code of N dimension
Euclidean Distance is the most common use of distance. In most cases when people said about distance , they will refer to Euclidean distance. Euclidean distance or simply 'distance' examines the root of square differences between coordinates of a pair of objects.
The interactive program below will enhance your understanding about Euclidean distance. Try usual input that you have learned in Pythagorean Theorem such as A = (0, 0) and B = (3, 4), then explore with your own input up to 6 dimensions.
Input coordinate values of Object-A and Object-B (the coordinate are numbers only), then press "Get Euclidean Distance" button. The program will directly calculate when you type the input.
|
|
|
Features
|
|
|
|
|
cost |
time |
weight |
incentive |
|
Object A |
0 |
3 |
4 |
5 |
|
Object B |
7 |
6 |
3 |
-1 |
Point A has coordinate (0, 3, 4, 5) and point B has coordinate (7, 6, 3, -1).
The Euclidean Distance between point A and B is
The pattern of Euclidean distance in 2-dimension is circular. When the sink is on the center, it forms concentric circles around the center.

Euclidean distance is a special case of
Minkowski distance
with
![]()
Pseudo code of Euclidean Distance
Given: vector x1 and x2, each vector is a coordinate in N dimension
function EuclideanDistance
dist=0
for d=1 to N // d = dimension
dist=dist+(x1[d]-x2[d])^2
next
return sqrt(dist )
end function
<Content | Previous | Next >
This tutorial is copyrighted.
Preferable reference for this tutorial is
Teknomo, Kardi (2015) Similarity Measurement. http:\people.revoledu.comkardi tutorialSimilarity