Linear Independent
In this page, you will learn more about linearly dependent and linearly independent vectors.
In the previous topic of
Basis Vector
, you have learned that a set of vectors can form a coordinate system in
dimensional space. The set of vectors that can form a coordinate system is called
basis vectors
. One main characteristic of basis vectors is that they cannot be put as a linear combination of other basis vector. This characteristic is called
linearly independent
vectors. Before we discus about linearly independent vectors, we will discuss about
linearly dependent
vectors.
Linearly Dependent Vectors
A set of vectors of the same
dimensions
is said to be
linearly dependent
if there is a set of scalars
, not all zero, such that the
linear combination
is a zero vector
.
Linearly dependent vectors cannot be used to make a coordinate system. Geometrically, two vectors are linearly dependent if they point to the same direction or opposite direction. These linearly dependent vectors are parallel or lie on the same line (collinear). Three vectors are linearly dependent if they lie in a common plane passing through the origin (coplanar).
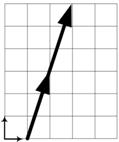
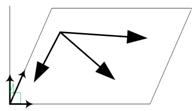
Algebraicly, we can augment the set of vectors to form a matrix
size
by
. If the matrix
is singular (i.e. it has no inverse), then we say that the set of vectors
are linearly dependent.
Linearly Independent Vectors
Having discussed about linearly dependent vectors, now we are ready for linearly independent vectors.
A set of vectors that is not linearly dependent is called linearly independent. When you put linearly independent vectors in the form of linear combination
, the only correct answer would be
because linearly independent vectors
cannot be put as a linear combination of one another. Since that is the main characteristics of basis vectors, we say that basis vectors are equivalent to
linearly independent
vectors.
Geometrically, linear independent vectors form a coordinate system.
By inspection we can determine whether a set of vectors is linearly independent or linearly dependent. If at least one vector can be expresed as a linear combination (i.e. scalar multiple or sum) of the other vectors, then the set of vectors is linearly dependent. If no vector can be expressed as a linear combination of the other vectors, then the set of vectors is linearly independent.
Examples:
A set of vectors
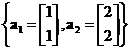is linearly dependent because we can expresed as a scalar multiple
.
A set of vectors
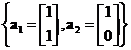is linearly independent because we cannot find a scalar
such that
.
A set of vectors
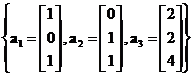is linearly dependent because we can expresed as a linear combination
.
Algebraicly, the vectors
comprising the columns of
by
matrix
size are linearly independent if and only if the matrix
is non-singular (i.e. it has inverse).
For two vectors
and
, simpler & faster computational procedure in a computer program is based on Cauchy-Schwartz inequality which stated that the absolute value of vector dot product is always less than or equal to the product of their norms
. The equality
holds if and only if the vectors are linearly dependent. Thus, the inequality indicates the vectors are the linearly independent.
The interactive program below is designed to answer whether two vectors are linearly independent or linearly dependent.
See Also : Basis Vector , Changing Basis , Eigen Values & Eigen Vectors
Rate this tutorial or give your comments about this tutorial