Scalar Multiple of a Matrix
When we multiply a real number
with a matrix
, we have the scalar multiple of
. The scalar multiple matrix
has the same size of the input matrix
and it is obtained by multiplying each element of
by
that is
.
Example
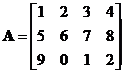
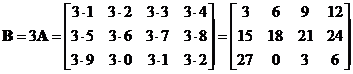
The interactive program below shows you the result of matrix scalar multiple. Your input is a matrix of any size but less than 100 scalar elements and a scalar number. Random Example will generate both random matrix and random scalar.
Properties
Some important properties of matrix scalar multiple are
-
Matrix scalar multiple is a commutative operation. When the order is reversed, you will still get the same result
-
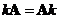
Matrix scalar multiple is an associative operation. You can exchange the order of computation (operation inside parentheses are to be computed first) does not change the result
.
-
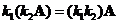Matrix scalar multiple is a distributive operation. You can distribute (and group) the scalar with respect to addition
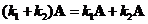and multiplication
.
-
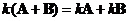Matrix scalar multiple is also an associative operation with respect to
matrix product
. You can exchange the order of computation (operation inside parentheses are to be computed first) does not change the result
.
-
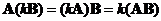When the scalar is zero, matrix scalar multiple will produce a
zero matrix
-
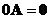
When the scalar is one, matrix scalar multiple will produce the input matrix itself
-
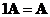
When the scalar is negative one, matrix scalar multiple will produce the negative of the input matrix
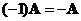
See also : matrix multiplication , matrix addition , matrix zero
Rate this tutorial or give your comments about this tutorial