Matrix Multiplication
One of the most important matrix operations is matrix multiplication or matrix product. The multiplication of two matrices
and
is a matrix
whose element
consists of the vector inner product of the
row of matrix
and the
column of matrix
, that is
. Matrix multiplication can be done only when the number of columns of
is equal to the number of rows of
.
If the size of matrix
is
by
and the size of matrix
is
by
, then the result of matrix multiplication is a matrix size
by
, or in short
.
Example
,
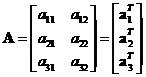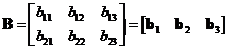
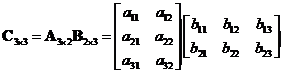
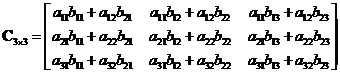
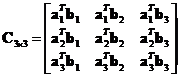
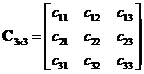
Example
,
Notice that the matrix multiplication produces
null matrix
even if the input two matrices are not null matrices.
The interactive program below shows you the result of matrix multiplication. Your input must be two matrices, one with size m by n and the other one with size n by k. Random Example will generate random matrices at the right size. Try to input your own matrices to gain more understanding about matrix product.
Properties
Some important properties of matrix multiplication are
-
Matrix product is an non-commutative operation. In general, you cannot reverse the order of multiplication
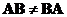. This is very different from multiplication of two numbers.
-
Matrix product is an associative operation. You can exchange the parentheses (to say which order to be computed first) and it does not change the result
.
-
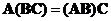Matrix product is a distributive operation. You can distribute (and group) the multiplication with respect to
addition
as long as the order of multiplication does not change,
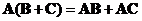and
-
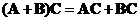
Identity matrix
is a multiplicative identity matrix such that
.
-
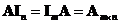Transpose
of the product of two matrices is equal to the product of their transposes taken in the reverse order
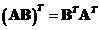. In general, the transpose of the matrix products can be extended to several matrices
-
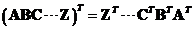
Determinant
of a matrix multiplication is equal to the multiplication of their determinant,
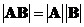
See also : matrix power , matrix inverse , vector inner product , Matrix element-wise product
Rate this tutorial or give your comments about this tutorial