Matrix Transpose
Transpose of a matrix is formed by interchanging the rows and columns of the input matrix.
If the input matrix size is m by n, the transpose matrix size is n by m.
Example:
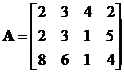
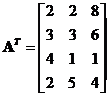
The notation of matrix transpose varies in the literatures, but in general we have three most used notation of matrix transpose:
or
, or
. In this linear algebra tutorial, I adopt the first notation because it's clearer in the eyes.
The interactive program below produces matrix transpose of the input matrix. Random Example button provide you will unlimited examples of random matrix. Play with the two buttons or type your own input matrix to gain more understanding about matrix transpose.
Properties
Some important properties of matrix transpose are
- Transpose of a (column) vector is a row vector and vice versa
-
The transpose of a transposed matrix returns the original matrix,
-
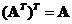
Transpose of the
summation
of two matrices is equal to the summation of their transposes
-
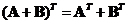
Transpose of the product of two matrices is equal to the product of their transposes taken in the reverse order,
-
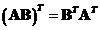
The transpose of the matrix
products
can be extended to several matrices
-
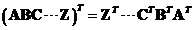
The
inverse
of a transpose matrix is equal to the transpose of its inverse,
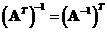
See also : matrix addition , matrix multiplication
Rate this tutorial or give your comments about this tutorial