What is Vector?
When you measure a physical quantity, you may get a number or a sequence of numbers in particular order.
A single number quantity to represent only the magnitude or the value of your measurement is called a scalar . Example: when you measure mass, work, speed, energy, temperature, density, and time and so on you will get a single number. Scalars can be compared only if they have the same units. For instance, you can compare a speed in km/hour with another speed in km/hour but you cannot compare a speed with a density.
A sequence of scalar numbers in certain order is called an array . Example: when you repeat your measurement in a day and record them in a sequence, you get an array of measurements.
An array of arrays that you arrange the scalar numbers into a rectangular table is called a matrix . Example: you repeat your measurements on different day and each day you measure exactly the same number of measurements, then you can put them into a table, that table is called a matrix. Thus, a matrix consists of m rows and n columns. You will learn more about matrix in later section of this linear algebra tutorial.
A special case of a matrix where it has only one row or one column is called a vector . Thus, from the arrangement point of view, a vector is just an array. But why don't we just call it an array instead of a vector? There is something special about vector. What is so distinctive about vector? You will find out more about vector in this section of the tutorial.
Before we go to the definition of a vector, let us take a look from how we distinct an array and a vector from computational point of view. In a computer program, an array is represented as a sequence of numbers in one dimensional array such as arr = [1, 2, 3, 4, 5]. We can take the first element (usually elements of array start counting from zero) is arr[0] = 1, the second element is arr[1] = 2 and the last element is arr[4] = 5. A vector is represented as
two-dimensional array
and element of vector is start counting from 1 (at least from the theory). The same array above if represented as a vector becomes vec = [1, 2, 3, 4, 5] and we should show the vector as
The first element is vec[1][1] = 1, the second element is vec[2][1] = 2 and the last element is vec[5][1].
Now we can show a simple operation that we cannot do it in array. We can transpose the column vector into a row vector like this
The first element of the row vector is rowvec[1][1] = 1, the second element is rowvec[1][2] = 2 and the last element is vec[1][5]. In this tutorial, you will find many more vector operations that we cannot do it in array.
Having distinguished an array from a vector, now we are ready to define what vector is.
A vector is defined as a quantity that requires both magnitude and direction in space. Examples of vector are displacement, velocity, acceleration, force, momentum, electric field and so on. Vectors can be compared if they have the same physical units and geometrical dimensions. For instance, you can compare 2-dimensional force with another 2-dimensional force but you cannot compare 2-dimensional force with 3-dimensional force. Similarly, you cannot compare force with velocity because they have different physical units.
The total number of elements in a vector is called the
dimension
or the
size
of the vector. Since a vector can have
number of elements, we say that the space where the vector lies is a multidimensional space with
dimensions.
The magnitude of a vector is sometimes called the length of a vector, or norm of a vector.
The direction of a vector in space is measured from another vector (i.e. standard basis vector), represented by the cosine angle between the two vectors.
The very simple interactive program below is designed to answer question whether your input is a vector or not according to the specified format of the program. Try to type your own input or use random example.
Unlike ordinary arrays, vectors are special that we can be viewed vectors in both algebra and geometric point of view.
Algebraically, a vector is just array of scalar elements. From computational point of view, a vector is represented as 2-dimensional array while ordinary array is represented as 1 dimensional array, as I have explained above.
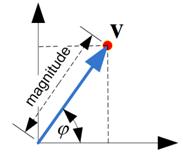
Geometrically, a vector is represented either as
an arrow
in space. A vector as an arrow can be translated along the line containing the vector (called
line of application
) and can be displaced parallel to that line of application and vector can also be applied to any point in space as long as the magnitude and direction does not change.
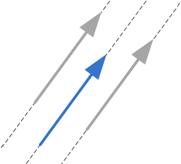
There is more about vector in geometry. A vector can also be represented a point in space. When a vector is represented as a point in space, we can also view that vector as an arrow starting at the origin of a coordinate system pointing toward the point. Because the coordinate system does not change, we only need to draw the points without the arrows.
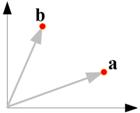
Using a vector as a point, now you can represent multidimensional value simply as one point in multidimensional space. This greatly simplified the complexity.
See Also : What is Matrix? , Resources on Linear Algebra
Rate this tutorial or give your comments about this tutorial