What is Matrix?
When you have a numerical data, you may want to put your data into a table.
For example: the unit price of land, labor and material in 4 cities is given in the following table
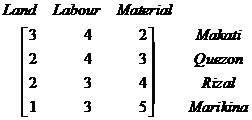
When you give name to your data table which consists of horizontal rows and vertical columns and think of it as one entity, you have a compact form that make it easier to manipulate your data and to automate the operations on your data using fast and efficient procedures to find the solution of your problem.
Since the meaning of each row and each column is well defined in each application, we can remove the definition and dealing only with the array of elements. The table above can be written as
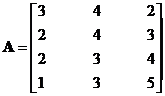
A collection of numerical data which is organized into rows and columns is called a matrix . A matrix is rectangular array of elements. A matrix is defined by its size that is the number of rows and the number of columns. We always write matrix size as number of rows first and then the number of columns. A square matrix happens when the number of rows is equal to the number of columns, the size can be written as one number called order of the matrix, that is equal to the number of rows = the number of columns.
Example:
A (m by n) matrix has m rows and n columns.
When m=2 and n = 3, we have for instance
Example:
A (n by n) matrix is a square matrix of order n. When n = 3, we have for instance
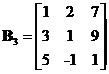
Based on the
matrix size
, we can give name:
A
rectangular matrix
is general matrix size m by n
A
square matrix
order n has equal size n by n (the number of rows is the same as the number of columns)
A
vector
is a matrix size m by 1 (any positive number of rows, but only one column)
A
row vector
is a matrix size 1 by n (any positive number of columns, but only one row)
In many modern books and journal papers, a matrix usually has notation of a bold uppercase roman letter, such as
,
,
, ...,
while a vector is written as bold lowercase roman letter such as
,
,
, ...,
. The entry element of a matrix or a vector is a scalar, usually denoted as lowercase roman letter.
For example
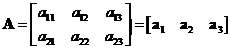
The following are some examples of useful ways to organize things into matrix:
-
One of the most useful matrix applications is to represent
simultaneous linear equations
. Consider a linear system
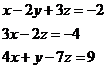
It can written as an augmented matrix that can be solved using Gauss Jordan method
-
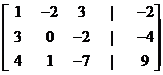
In some data matrix, each row in a matrix usually represents an object or one observation, while each column of a matrix usually indicates features (or attributes or variables).
-
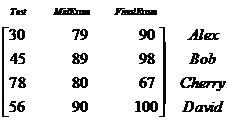
In distance matrix, each row and each column represents the same object, the element of the matrix indicate the distance between objects. The distance matrix is a
symmetric matrix
.
-
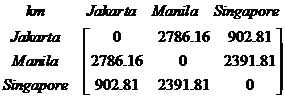
A matrix can also represents observations in rows and other observations in columns, or some attributes in rows and some other attributes in columns.
-
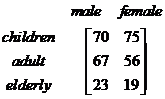
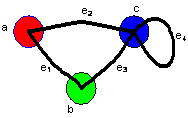
Some types of matrices are closely related to
graph theory
. The rows or columns can represent the nodes or links in a graph. For example, the
incidence matrix
below is associated with the 3 nodes and 4 links graph.
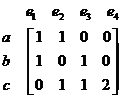
- Probability matrix contains probability to move from one position to the next position.
Rate this tutorial or give your comments about this tutorial