Determinant
Each n by n square matrix 
has an associated scalar number, we called as determinant of that matrix, whose value will determine whether the matrix has an inverse or not. The symbol of determinant is either 
or
.
When matrix order is 1, 
then 
When the matrix order is 2,
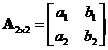, then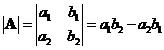 
When the matrix order is 3,
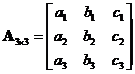, then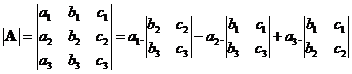 
When we have a matrix
then we can define several things:
- The minor of
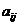is the determinant of a 
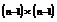sub matrix denoted by 
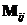. The sub matrix 
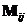obtained from matrix
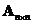by deleting the row and column containing
.
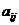Example: we have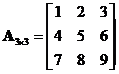
then the sub matrix of 
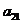is 
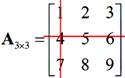or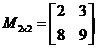
and the minor is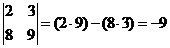 
- The signed minor is called cofactor of
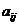denoted by
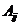. Cofactor is a scalar sign determined by
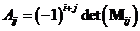. This sign follows the following order
Example:
Suppose we have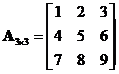 
then the cofactor of 
is
The determinant of matrix 
is the sum product of the first column entries with its cofactor, that is 
For example,
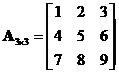, then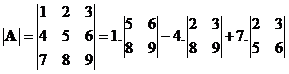 
Hand (manual) computation of determinant of matrix size larger than 3 is quite time consuming. The interactive program below will help you to compute determinant of your square matrix of any positive order less than 10. Random Example button will generate random square matrix of random size.
Properties
The following are well known properties of matrix determinant:
- A square matrix
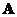is singular (has no inverse) if and only if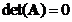 
- If a square matrix
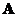has an inverse, the determinant of an inverse matrix is the reciprocal of the matrix determinant, that is
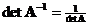. - When matrix
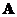has a row or a column consisting entirely of zeros, then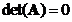 
- When matrix
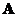has two identical rows or two identical columns, then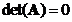 
- Determinant of a matrix product is equal to the product of their determinant,
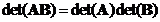
- Determinant does not change when we transpose the matrix,
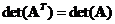
- Determinant does not change when we add a multiple of a row or a column to another.
- Interchanging two rows or two columns of a matrix changes the sign of the determinant but the magnitude of the determinant does not change.
- Multiplying a row or a column of a matrix by a scalar will make the value of the determinant multiplied by that scalar. Similarly, removing a common factor from a row or a column will also remove the common factor from its determinant.
- When matrix
is an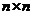
triangular matrix, the determinant equals the product of the diagonal elements of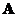
See also: matrix product, matrix inverse, matrix transpose, and elementary row operations, matrix trace, matrix rank, Rotation or Reflection
Rate this tutorial or give your comments about this tutorial
Preferable reference for this tutorial is
Teknomo, Kardi (2011) Linear Algebra tutorial. https:\\people.revoledu.com\kardi\tutorial\LinearAlgebra\